COME ESEGUIRE LA VERIFICA CON IL "METODO GENERALE"

Con il nome di "metodo generale" si intende la verifica della interazione tra resistenza e stabilità condotta mediante un metodo che generalizza quanto si fa per il caso di semplici colonne compresse. Il metodo è descritto in EN 1993-1-1 al §6.3.4 relativamente allo svergolamento di travi inflesse, ma è di fatto adoperato anche in numerosi altri contesti all'interno della norma in questione. Il metodo è descritto e discusso nel testo Calcolo di Strutture in Acciaio, di Paolo Rugarli, EPC Libri, 2008, al §1.7.1 e verrà ora brevemente richiamato.

Sia data una generica struttura e consideriamo una generica combinazione di carico ad essa associata. Sia αcr il moltiplicatore critico (positivo), ovvero il moltiplicatore dei carichi che conduce alla instabilizzazione di tutta o di parte della struttura. Sia inoltre αu il moltiplicatore limite, ovvero il moltiplicatore dei carichi (positivo) che porta alla creazione di un meccanismo, ovvero alla formazione di un atto di moto rigido all'interno della struttura a seguito della plasticizzazione di uno o più dei suoi elementi resistenti (cerniere plastiche o plasticizzazione di elementi tesi o compressi). Definiamo col termine generale di criticità, o snellezza adimensionale, il numero adimensionale λ ottenuto dalla seguente epsressione

      (1)

Data la criticità e data una curva di stabilità, ovvero una relazione del tipo χ=χ(λ) è possibile determinare un fattore di riduzione χ che dipende dalla criticità e che va a diminuire il carico che, in assenza di fenomeni di instabilità, si potrebbe applicare sulla struttura. Dunque il moltiplicatore reale dei carichi, non è αu ma è αR  e vale

       (2)

Il metodo è applicabile a qualsiasi struttura e tiene conto del fatto che, a causa dei fenomeni di instabilità, il carico per resistenza idealmente raggiungibile può non essere raggiunto. E' importante osservare che il concetto di criticità (ed il calcolo di χ) è totalmente svincolato da concetti come lunghezza, distanza tra i punti di flesso, ed è associabile a qualsiasi struttura, come un guscio, una lastra, una copertura, ecc..

 Un punto di fondamentale importanza nella applicazione del metodo è la scelta della curva di stabilità. Normalmente si adoperano le stesse curve di stabilità impiegate per la verifica di elementi compressi (curve a0, a, b, c, d), dato che tali curve di stabilità rendono conto di diversi possibili livelli di imperfezione e costituiscono una stima ingegneristica della maggiore o minore probabilità che si inneschino i fenomeni di instabilità stessi. La curva di stabilità è associata ad un fattore di imperfezione che vale 0,13 per la curva a0, 0,21 per la curva a, 0,34 per la curva b, 0,49 per la curva c, ed infine 0,76 per la curva d. E' naturalmente possibile definire altre curve pur di impostare valori differenti per il fattore di imperfezione (si veda la Tabella 6.1 di EN 1993-1-1).

 Per poter applicare il metodo occorre quindi conoscere il fattore αcr  ed il fattore αu . Si noti che è sempre a favore di sicurezza sottostimare αu, dato che se è vero che la criticità viene ad essere sottostimata (perché αu compare a numeratore nella (1)) è anche vero che nella espressione (2) l'effetto finale sarà una sottostima e non una sovrastima di αR. In altre parole le curve αR=αR(αu) sono sempre crescenti per ogni αcr. Questo vuol dire che ai fini di una determinazione a favore di sicurezza di αR è possibile usare una sottostima di αu quale quella ottenuta con metodi semplificati e senza bisogno di ricorrere ad una vera e propria analisi limite.

Curva a0

Nella precedente figura, ad esempio, si vede il rapporto tra αu ed aR per valori diversi di αcr e per la curva a0. Come si vede sottostimare αu porta anche a sottostimare aR, il che è a favore di sicurezza. Nelle figure successive vengono riportati gli analoghi abachi per le curve di stabilità a, b, c, e d.

Curva a

Curva b

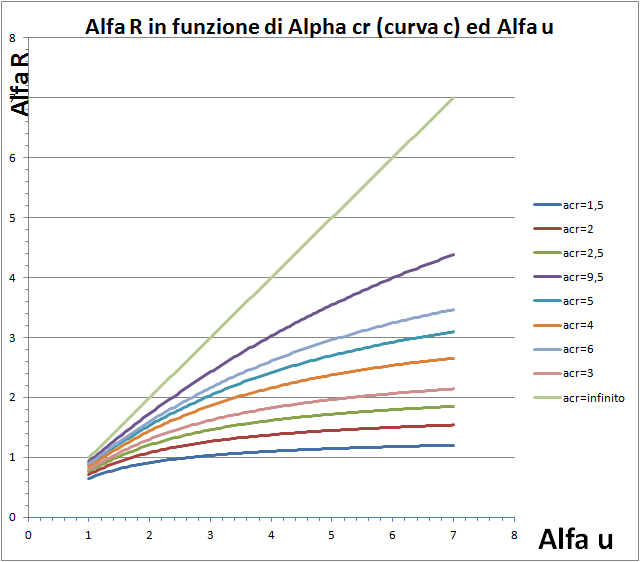
Curva c

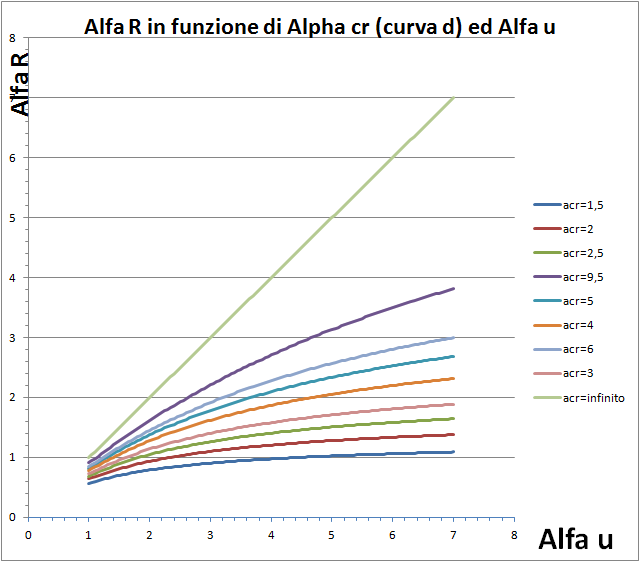
Curva d

La stima di αu può essere fatta in modo semplificato come segue.

Si può considerare il moltiplicatore dei carichi che porta una sezione di qualche elemento (biella o trave) al limite elastico. In tal caso αu=α1, ovvero si raggiunge il primo snervamento di qualche elemento. In tal caso, usando un criterio semplificato |N/A|+|M2/W2|+|M3/W3|=fy.

Oppure si può considerare il moltiplicatore dei carichi α1y che porta una sezione di qualche elemento alla piena plasticizzazione, ed in tal caso |N/A|+|M2/W2,pl|+|M3/W3,pl|=fy.

In altri casi αu può essere valutato mediante considerazioni basate su analogie come la stessa normativa prevede (§7.4.3.2., §7.5.2.2, ecc.) facendo variare αu/α1 da 1,0 a 1,3.

 I ragionamenti fatti si qui per una generica combinazione, devono essere ripetuti per tutte le combinazioni. Sargon, a partire dalla versione 10,0 constente appunto di far ciò, mediante un opportuno comando, detto Metodo Generale, e posto sotto il menu Post-Buckling.

 Dato che una precedente analisi di buckling ha determinato per ogni combinazione "i" il suo (primo) moltiplicatore critico αcr,i, supposto positivo, il programma è in grado di valutare per ogni combinazione una stima semplificata di αu,i e quindi per ogni combinazione "i" una stima di αR,i.

 Nella figura seguente si vede un caso studiato mediante tale comando.

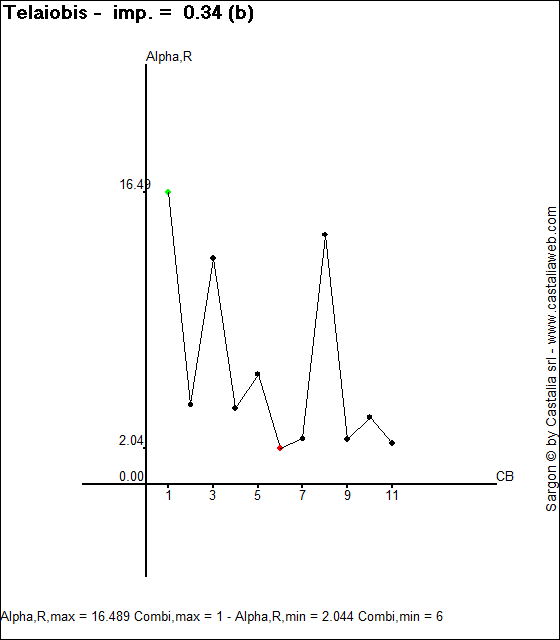
Come si vede l'αR è qui compreso tra 16,49 per la combinazione 1 e 2,04 per la combinazione 6. La verifica è positiva in quanto αR> 1 (si noti che è stata usata la curva b). Il seguente tabulato, ottenibile mediante il medesimo comando, spiega i calcoli in dettaglio:

----------------------------------------------------

-                                                  -

-                  General Method                  -

-                                                  -

-                                                  -

- Sargon © by Castalia srl - www.castaliaweb.com   -

----------------------------------------------------

Model name:               Telaiobis

Number of combinations:      11

Imperfection factor:       0.34

Combi     Alpha,u        Alpha,cr      Lambda,s         X         Alpha,R  

    1   3.955e+001     2.267e+001    1.321e+000    4.169e-001   1.649e+001

    2   1.608e+001     5.615e+000    1.692e+000    2.802e-001   4.506e+000

    3   4.021e+001     1.632e+001    1.570e+000    3.178e-001   1.278e+001

    4   1.638e+001     5.297e+000    1.758e+000    2.624e-001   4.299e+000

    5   2.073e+001     7.857e+000    1.624e+000    3.003e-001   6.224e+000

     6   8.084e+000     2.504e+000    1.797e+000    2.528e-001   2.044e+000

    7   1.002e+001     3.183e+000    1.775e+000    2.583e-001   2.589e+000

    8   4.012e+001     1.842e+001    1.476e+000    3.513e-001   1.409e+001

    9   1.013e+001     3.112e+000    1.804e+000    2.510e-001   2.543e+000

   10   1.398e+001     4.715e+000    1.722e+000    2.720e-001   3.804e+000

   11   9.146e+000     2.871e+000    1.785e+000    2.558e-001   2.339e+000

Combi,min:      6  -  Alpha,R,min = 2.044

Se si fosse usata la curva d, si sarebbe ottenuta la immagine seguente, con un moltiplicatore reale massimo pari a 1,70.

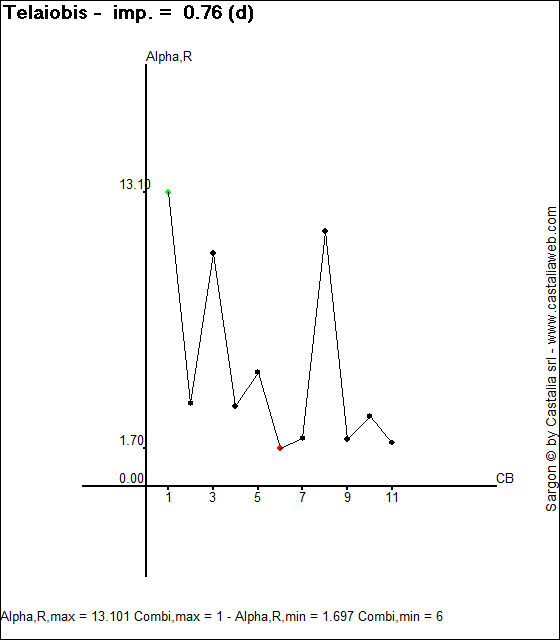
Lo studio di queste curve è particolarmente interessante per capire, al di là delle mere apparenze, quali sono le combinazioni di carico potenzialmente più pericolose per una certa struttura.

 Prima di eseguire questo comando è bene accertarsi che tutti i primi modi critici di tutte le combinazioni abbiano moltiplicatore critico maggiore o eguale a zero (eseguendo il comando Interroga). Se ciò non avviene e si hanno uno o più primi moltiplicatori negativi, per una o più combinazioni, o si cercano moltiplicatori positivi aumentando l'ordine del sottospazio, oppure si deseleziona la combinazione, scartandola da quelle indagate.

 A partire dalla versione 12.70 sono indicati i risultati relativi ai primi tre moltiplicatori critici.