COMBINAZIONE DEI MODI E FATTORE DI ERRORE (PROPERTY PAGE)

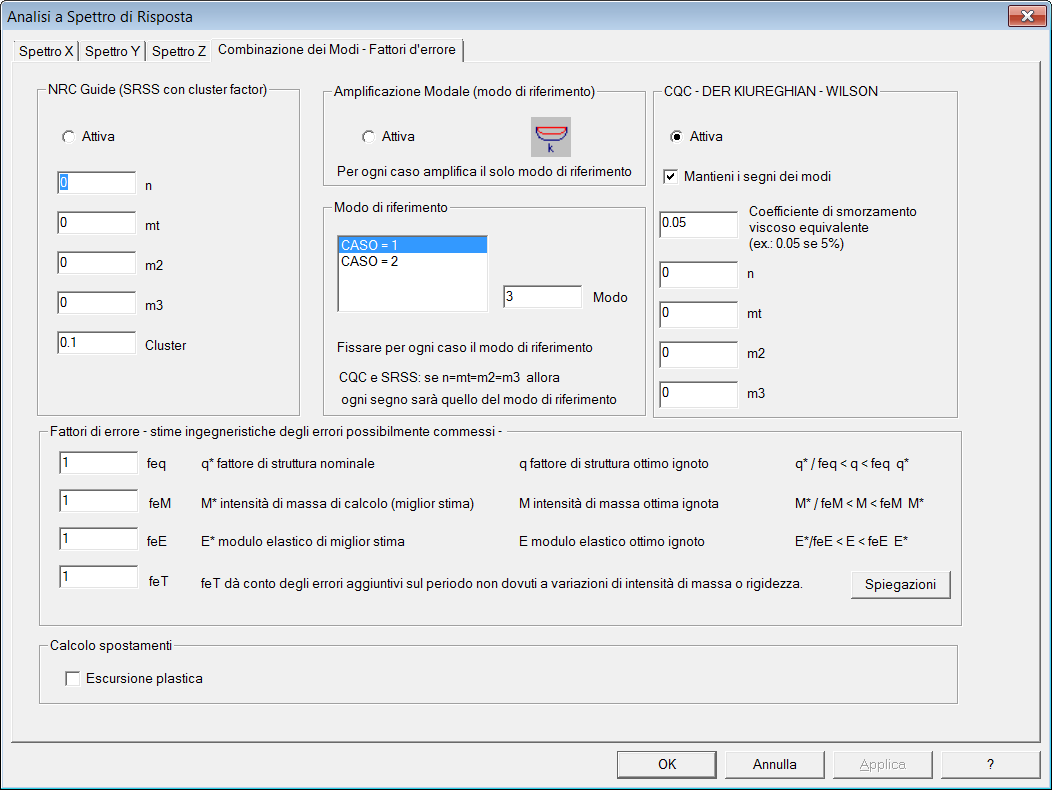
 Questa property page fa decidere in che modo l'effetto dei vari modi verrà combinato per dare il risultato complessivo (cfr. anche Analisi a spettro di risposta con SPECTRUM).

 I metodi possibili sono tre: il metodo NRC, il metodo dell'amplificazione modale ed il metodo della Complete Quadratic Combination (CQC) . Il metodo desiderato viene scelto accendendo il flag attiva corrispondente.

 Per ogni caso di carico di tipo sisma modale è possibile indicare un modo di riferimento. Tale modo di riferimento, se indicato, sarà impiegato per determinare i segni degli spostamenti, delle reazioni e delle azioni interne. Se invece il modo di riferimento è 0, allora non sarà inizialmente eseguita alcuna correzione.

 Una ulteriore correzione è poi eseguita opzionalmente e dipende dai valori dei parametri n, mt, m2 ed m3. Se essi sono nulli i segni corrispondenti non saranno modificati (e rimarranno o indisturbati, se per quel caso di carico non è stato specificato alcun modo di riferimento, o eguali a quelli del modo di riferimento se questo è stato indicato).

 n indica se dare o meno correzione al segno dell'azione assiale: 0 indica nessuna correzione, un numero negativo indica che le azioni assiali saranno negative, un numero positivo indica che le azioni assiali saranno negative. Tutti gli elementi saranno dunque tesi (n > 0) o compressi (n < 0).

 mt indica se dare o meno correzione al segno del momento torcente: 0 indica nessuna correzione, un numero negativo indica che i momenti torcenti saranno negativi, un numero positivo indica che i momenti torcenti saranno positivi.

 m2 indica se correggere o meno il momento flettente secondo l'asse locale 2. 0 indica nessuna correzione, un numero positivo corrisponde a un diagramma in cui il momento ha sempre lo stesso segno. Un numero negativo corrisponde a un diagramma “a farfalla”. In entrambi i casi il taglio T3 verrà ricalcolato in modo da far equilibrio ai momenti ottenuti combinando i modi. Se non si vuole questa correzione occorre dare il valore 0 (e in questo caso tagli e momenti non saranno più in equilibrio).

 m3 indica se correggere o meno il momento flettente secondo l'asse locale 3. 0 indica nessuna correzione, un numero positivo corrisponde a un diagramma in cui il momento ha sempre lo stesso segno. Un numero negativo corrisponde a un diagramma “a farfalla”. In entrambi i casi il taglio T2 verrà ricalcolato in modo da far equilibrio ai momenti ottenuti combinando i modi. Se non si vuole questa correzione occorre dare il valore 0 (e in questo caso tagli e momenti non saranno più in equilibrio).

 cluster indica il fattore di cluster (0.1 = 10%).

 mantieni i segni dei modi è un flag che se attivato comporta il fatto che nella CQC gli effetti dei singoli modi siano presi col segno. Ciò comporta il fatto che i doppi prodotti pesati dal coefficiente di correlazione possano anche essere negativi. Se invece il flag è spento, allora verranno usati i valori assoluti, il che dà sempre luogo a doppi prodotti positivi.

Coefficiente di smorzamento viscoso equivalente: è un numero puro in genere pari a qualche percento. E’ usato nel metodo della CQC per calcolare il coefficiente di correlazione modale.

 Modo indica quale modo amplificare per il caso di carico selezionato nella lista posta immediatamente a sinistra.

_____________________________

Fattori di errore

A partire dalle versione 7.1 la soluzione mediante il metodo dello spettro di risposta viene eseguita – a richiesta – anche secondo il metodo dello spettro di risposta con fattore di errore. Per una estesa trattazione del tema, si rimanda all’articolo allegato: Spettro di risposta con fattore di errore.

 Il fattore di errore è un numero che è considerato in genere maggiore di 1 e dà conto del fatto che una certa grandezza al valore nominale, d* , possa invece assumere un valore da questo diverso. Pertanto il programma indaga cosa succede se  il valore “reale” d è più basso (d*/f) oppure più alto (d*f) di quello nominale d*.

 Il fattore di errore non è né potrebbe essere un numero “rigoroso”, probabilistico o “esatto”, ma solo una (peraltro fondamentale) stima ingegneristica, motivata da considerazioni che dipendono dal singolo problema in esame. Il fattore di errore è un grado di libertà che il progettista mantiene per sé e che serve ad indagare situazioni prossime, ma non simili, a quelle allo studio.

 Vengono definiti i seguenti fattori di errore:

Sul fattore di struttura (feq). Ovviamente il fattore di struttura “di calcolo” risulterà pari a q*/f, essendo a favore di sicurezza il numero minore. Porre fq=1 significa non variare il coefficiente di struttura nominale.

Sulla intensità di massa a parità di distribuzione (feM). In genere spostamenti e sollecitazioni aumentano con la massa, e quindi generalmente il programma finirà con l’adottare una risposta con un livello di massa pari a M*feM.Porre feM=1 significa non variare la intensità di massa. Questo fattore di errore è a parità di distribuzione, e quindi non c’entra nulla con l’eccentricità accidentale, che dovrà essere studiata a parte.

Sulla intensità del modulo elastico (feE). In pratica la rigidezza viene variata in modo omogeneo a parità di distribuzione. Ciò viene fatto anche quando nel modello compare più di un materiale. Non esiste un caso valido in generale. Gli spostamenti tendono a diminuire all’aumentare di E, ma le azioni interne restano invariate o aumentano. Porre feE=1 significa non variare il modulo di elasticità e quindi non variare la rigidezza.

Sul periodo (feaT) a causa di errori non dipendenti dalla intensità di massa o di rigidezza. Tale fattore di errore tiene in conto le incertezze sul periodo di calcolo dovute alla discretizzazione alle dimensioni geometriche, ecc..

In generale, detto T il periodo di un modo, C il suo coefficiente di risposta, X lo spostamento ad esso associato, e F la azione interna ad esso associata, valgono le seguenti espressioni per i fattori di errori derivati:

       (*)

feC=feC(T, feaT, feM, feE, feq) una funzione che dipende dallo spettro adottato

feX=feCfeT2

feF=feMfeC

Il programma calcola dapprima dei periodi « lower bound » ed « upper bound » grazie alla (*). Da questi può valutare dei coefficienti di risposta “lower bound” e “upper bound” e quindi dei fattori di erorre su C, feC. Fatto ciò, il programma indaga sugli spostamenti e sulle azioni interne mediante le due formule indicate, e quindi perviene ai massimi valori (>1) per feX ed feF. A questo punto i valori “nominali” degli spostamenti saranno amplificati da feX, mentre i valori nominali degli sforzi saranno amplificati da feF. Il risultato è una sovrastima a favore di sicurezza, tenendo in conto possibili variazioni di fattore di struttura, della intensità di massa a parità di distribuzione, della intensità di rigidezza a parità di distribuzione, del periodo a causa di errori diversi da quelli indicati.

Poiché in generale feX ed feF saranno diversi, è normale che gli spostamenti in uscita non siano “coerenti” con le azioni interne calcolate sul modo. Il programma prende le variazioni che comportano, separatamente, il caso peggiore (spostamenti maggiori, azioni interne maggiori).

Un volta calcolati gli effetti modali in questo modo, questi vengono poi combinati per le vie normali.

Valori da adottare per i fattori di errore

Ovviamente dipende dalle circostanze, dal tipo di struttura ecc. Si possono comunque dare le seguenti indicazioni di larga massima.

Fattore si struttura.

Nei casi più fortunati, ovvero strutture simili a quelle studiate in letteratura, regolari, normate, un 10% di errore sul fattore di struttura sembra il minimo, pertanto nei casi più fortunati 1.1 per fq.

Massa

Se la struttura è stata accuratamente modellata (anche per le masse non strutturali), e i variabili sono modesti ci si può limitare a un 5% (fm=1.05). Nel caso in cui le masse siano state valutate grossolanamente e/o i variabili siano molto importanti, fm=1.1-1.2. Errori maggiori suggeriscono di migliorare il modello o di indagare varie possibili configurazioni di variabili.

Rigidezza

Per strutture in acciaio nelle parti rilevanti, feE=1.02-1.05. Nel caso del calcestruzzo almeno feE=1.1, ma anche feE=1.3 dipendentemente dal tipo di garanzia sulla qualità del calcestruzzo che si può pensare di ottenere.

Periodo (errori aggiuntivi)

Del tutto ineluttabile appare un feaT=1.05. Nel caso di strutture rozzamente modellate, o prive di estremi rigidi benchè funzionanti a telaio, anche feaT=1.1-1.2.

_____________________________

Calcolo spostamenti

Nei casi in cui sia definito un fattore di struttura, il calcolo degli spostamenti e delle azioni interne avviene in coerenza con uno spettro di risposta elastico ridotto mediante il fattore di struttura q. Mentre le azioni interne sono "corrette" nel senso che tengono conto della duttilità, gli spostamenti non sono coerenti con quanto si otterrebbe sull'oscillatore semplice, dato che gli spostamenti effettivi sono molto maggiori di quelli ottenuti con lo spettro di progetto (ovvero lo spettro elastico ridotto dal fattore di struttura q). Essi si ottengono moltiplicando gli spostamenti coerenti con lo spetrto di progetto per un fattore μ. Normalmente gli spostamenti "plastici" sono coerenti con quelli dello spettro elastico (regola di egual spostamento, posto T1 come periodo del modo considerato, se T1 > TC) e allora μ=q, ma in certi casi il fattore μ può essere maggiore di q (quando T1 < TC). Se gli spostamenti "effettivi" (ovvero quelli plastici) devono essere utilizzati per le verifiche si hanno due possibilità.

1) Si calcolano gli spostamenti ridotti dal fattore di struttura q e poi ci si ricorda di moltiplicare tali spostamenti per μ ogni volta che vengono utilizzati.

2) Si calcolano gli spostamenti senza ridurli per il fattore q e si usano direttamente per le verifiche.

 Per default il programma segue l'approccio 1), ovvero utilizza lo spettro di progetto sia per le azioni interne che per gli spostamenti. In questo modo gli spostamenti danno luogo alle azioni interne calcolate, con l'ordinario legame sforzi-deformazioni. E' tuttavia possibile attivare l'approccio 2, ed in tal caso le azioni interne e le reazioni vincolari saranno calcolate con lo spettro di progetto, mentre gli spostamenti con lo spettro elastico. Per attivare l'opzione 2) occorre porre un segno di spunta nella casella "escursione plastica".