Come… eseguire analisi di pushover e di verifica delle capacità
Inquadramento
Pushover: una analisi per tutti i fini
La analisi di pushover (PA) è stata introdotta nella nostra normativa ormai 12 anni fa, nel 2003, con la Ordinanza PCM 3274/2003. Considerata da molti ambienti accademici e non come una specie di anello intermedio tra l'analisi modale e la time history non lineare, essa mostra soprattutto molti limiti, che però spesso vengono taciuti volentieri in vista dell'ottenimento di una serie di risultati molto suggestivi e tali da far apparentemente trarre conclusioni molto importanti.
Di fatto l'analisi fa uso delle forze apparenti coerenti con una analisi modale e a spettro di risposta, per caricare la struttura in modo da portarla a collasso. Quindi, il punto di partenza di una analisi di pushover è sempre una analisi modale, che dà luogo tramite spettro di risposta a forze che sono impiegate, opportunamente riscalate, per snervare sino al collasso la struttura.
Nella sua versione originale, la PA fa uso di un solo modo, quello dominante, e quindi ai fini della individuazione del sistema di forze fa implicitamente uso di un modello a un grado di libertà (SDOF). Tale forte ipotesi è anche mantenuta per ottenere da un sistema a molti gradi di libertà una sola curva di tipo carico-spostamento, la quale è impiegata per ottenere le caratteristiche meccaniche di un sistema SDOF (massa e rigidezza). Lo spostamento è quello di un particolare nodo strutturale, detto nodo di controllo, e la forza è il taglio alla base applicato, ovvero, in buona sostanza, la risultante delle forze ottenute con la analisi a spettro di risposta, moltiplicate per un fattore amplificativo variabile.
Scopo della analisi è determinare lo spostamento richiesto al sistema e da questo ottenere le duttilità di curvatura ed altre misure di impegno cinematico locali, che devono poi essere raffrontate con opportune soglie dipendenti dalla tipologia strutturale (ad esempio, travi o colonne in c.a., travi o colonne in acciaio, edifici con o senza tamponamenti, e così via) e dallo stato limite considerato.
La ragione per cui questa sezione è così intitolata è da ricercare nell'ampio spettro di compiti che è assegnato a questa analisi, anche quando mancherebbero le premesse per poterla applicare. Così, in letteratura si vede scritto che la pushover:
•è utile per determinare i fattori di struttura da assegnare a una certa costruzione (magari incapace di comportamento plastico);
•è utile per stimare la domanda di duttilità globale e locale e la progressiva invasione della plasticità nella struttura;
•è utile per dare più margini a strutture (esistenti) che altrimenti con altri sistemi sarebbero condannate, e quindi è il sistema di elezione per strutture esistenti.
•... e così via.
Tali generose generalizzazioni dimenticano volentieri i considerevoli limiti della analisi, in parte legati alla incertezza dei dati di ingresso (tipicamente gli spettri, e i periodi, i legami costitutivi, il contributo delle parti non strutturali, le masse, eccetera) ed in parte intrinsecamente legati al metodo in quanto tale, anche in presenza della divinatoria capacità di valutare con precisione i dati di ingresso: effetto delle irregolarità in pianta ed elevazione, perdita di linearità all'attingimento della prima plasticizzazione, effetti legati alla variabilità dei risultati con il nodo di controllo, con la distribuzione delle forze, eccetera.
Tipologie di pushover
Essendo chiari a tutti i limiti della analisi di pushover classica, non ultimo tra i quali il fatto che non vi sono motivazioni teoriche effettivamente coerenti e solide dietro di essa, negli anni sono state proposte diverse metodologie atte a superare, nelle intenzioni di chi le ha proposte, i limiti originari.
Le principali metodologie proposte come alternativa o integrazione alla PA unimodale classica sono:
•Le analisi di PA multimodali, le quali eseguono una PA unimodale su vari modi importanti separatamente, e poi calcolano un risultato finale, per ogni grandezza di interesse, mediante tecniche di SRSS o CQC.
•Le analisi di PA adattive, che ricalcolano i modi e le ordinate spettrali, nonché la distribuzione delle forze, via via che l'analisi progredisce in campo plastico.
Entrambi i rimedi sono discutibili.
Il primo perché eredita la approssimazione basata sulla radice quadrata del vecchio metodo di analisi a spettro di risposta, per di più con errori che si rivelano molto forti su strutture irregolari.
Il secondo perché a fronte di un significativo maggior onere computazionale non ha da offrire molto in termini di miglior metodologia, giacché alcuni limiti sostanziali del metodo, come l'uso di un solo punto di controllo e la variabilità dei risultati in sua funzione, la necessità di strutture altamente regolari, e l'uso di un solo modo anziché tutti, restano sostanzialmente immutati.
Criticità legate all'uso della pushover
Sebbene propagandata come panacea, l'analisi di pushover dà informazioni affette da gravi errori rispetto ai risultati ottenibili con time history non lineare. Ciò è in specie vero per la stragrande maggioranza delle strutture esistenti che sono altamente irregolari in pianta e spesso in elevazione e non dispongono di un comportamento duttile tale da consentire una vera analisi plastica.
Sargon la include per evitare che i propri clienti se ne trovino sprovvisti a fronte di richieste in questo senso provenienti dalle terze parti, ma deve essere chiaro che l'analisi in questione dà risultati sempre da considerare con critica attenta. Non solo sul fronte della domanda, stimata mediante le metodologie che sono state brevemente richiamate, ma anche sul fronte della capacità, dove la proposta di valori di soglia per gli spostamenti relativi di interpiano e per i valori limite della rotazione rispetto alla corda, deve essere coniugata con la estrema variabilità del costruito, l'effetto benefico o malefico delle parti non strutturali, l'interazione tra le varie componenti di sollecitazione (spesso trascurata o valutata sommariamente, in specie dai modelli a plasticità concentrata), l'incertezza sulle leggi costitutive, eccetera. Pertanto assegnare la suggestiva etichetta di "stato limite di collasso" al raggiungimento di certe soglie di drift di piano o di rotazione plastica, appare come una sostanziosa convenzione più che come una puntuale attribuzione di una qualifica sulla base di comportamenti misurabili.
Scopo della analisi di pushover
Scopo della analisi di pushover è trovare il punto di prestazione, o performance point, sulla curva unidimensionale carico-spostamento. A tale punto corrisponderà un campo di spostamenti e deformazioni nella struttura 3D originaria (domanda), che potrà essere puntualmente raffrontato con le soglie previste per ciascun stato limite (capacità).
Il performance point viene trovato stabilendo una analogia con il comportamento di un oscillatore elasto-plastico equivalente.
Sono fondamentali:
•La rigidezza e la massa del sistema equivalente (vari i criteri possibili per stabilire la equivalenza).
•Lo spettro di risposta adoperato per l'oscillatore equivalente e la domanda di spostamento ad esso associata (sito, PGA, effetti di suolo ecc.: hazard sismico).
•La corretta modellazione del comportamento strutturale (masse, rigidezze, leggi costitutive, sorgenti delle non linearità).
•La significatività del punto di controllo.
•La distribuzione (costante, lineare, modale, ecc.) delle forze applicate.
Limiti di applicabilità
Di fatto la struttura dovrebbe essere altissimamente regolare, e tale quindi da appiattirsi in modo sostanziale sul comportamento del primo modo. Effetti multimodali o torsionali abbattono considerevolmente la affidabilità del metodo.
I piani dovrebbero essere membranalmente rigidi, in modo da poter considerare un punto di controllo come effettivamente rappresentativo.
La modellazione delle leggi costitutive e delle sedi di plasticizzazione deve essere accurata. Si dovrebbe tener conto della interazione tra le varie componenti di sollecitazione, cosa assai difficile con modelli a cerneiere plastiche concentrate (Sargon usa invece la plasticità diffusa, con modelli a fibre).
La determinazione delle soglie di spostamento locale e di drift (capacità) in funzione della tipologia strutturale dovrebbe essere molto attenta, o in alternativa si dovrebbero considerare opportuni margini di incertezza.
Lo studio della sensitività della risposta alla scelta del punto di controllo, della distribuzione ed intensità di massa, delle modalità di stabilire l'equivalenza con l'oscillatore semplice, delle distribuzioni di forze, e delle forme spettrali (hazard sismico) sarebbe consigliata, ma porterebbe a un onere computazionale forte, in parte mitigato, usando Sargon, dalla disponibilità di comandi specifici.
La preparazione del modello di partenza
Stati limite e terremoti
Normalmente, ad ogni diverso stato limite deve essere associato uno spettro di risposta (nelle sue tre componenti X, Y e Z), figurativamente in relazione con un certo possibile terremoto di progetto. L'analisi di pushover, comunque, utilizza solo le direzioni X ed Y.
Se si devono eseguire le verifiche per ogni stato limite, a ciascuno stato limite dovrà essere associato un certo livello di severità di scuotimento.
A tale severità di scuotimento sarà possibile associare un performance point mediante una specifica analisi pushover, ed eseguire le verifiche di capacità locali conseguenti (drift di piano, elongazioni delle bielle o loro accorciamenti, e rotazioni plastiche).
In tal modo:
1.Ad ogni terremoto corrispondono varie analisi di pushover, corrispondenti alle diverse direzioni del sisma (X ed Y) ed alle diverse scelte delle modalità di esecuzione delle analisi di pushover (ad esempio la distribuzione delle forze lungo l'altezza della struttura).
2.Ad ogni singola analisi di pushover corrispondono una quantità di "prestazioni", ciascuna letta localmente in corrispondenza agli elementi dissipativi e ai drift di piano.
3.Tutte queste verifiche devono essere contemporaneamente soddisfatte.
Prerequisiti per le analisi di pushover
Dato che le analisi di pushover sono analisi non lineari, è necessaria la disponibilità del modulo non lineare CURAN. La versione CURAN LIGHT è sempre disponbile e tratta la non linearità di materiale e geometrica di elementi biella e molla. Per la non linearità di materiale degli elementi beam (trave, modello a fibre) è necessaria la versione FULL di CURAN.
Pertanto:
•Per strutture CBF (Concentrically Braced Frames) o BRBF (Buckling Restrained Bracing Frames) si può usare CURAN LIGHT, sempre disponibile.
•Per strutture MRF (Moment Resisting Frames) ed EBF (eccentrically Braced Frames) è necessario disporre di CURAN FULL.
Preparazione del modello per le pushover
Dato un modello originario usato per le normali analisi statiche e modali, questo deve essere opportunamente preparato, verosimilmente salvandolo con altro nome, ai fini delle analisi di pushover. Questo modello modificato sia il modello "padre".
La preparazione del modello comporta essenzialmente i seguenti passi:
•Attribuzione di materiali non lineari a tutti quegli elementi che potrebbero snervarsi sotto l'azione dei carichi di pushover applicati. Qui è molto importante anche che le soglie di deformazione ultima siano realistiche perché al loro attingimento corrisponde la rottura (di fibre per gli elementi beam, o di elementi per i truss). Si possono scegliere modelli costitutivi perfettamente plastici o incrudenti. Ovviamente la risposta ne sarà fortemente influenzata.
•Incremento della discretizzazione nelle zone dove sono verosimili cerniere plastiche (elementi beam), al limite, nella intera struttura. Una buona scelta, per le ragioni chiarite più sotto, è dividere in elementi in modo che l'elemento strutturale sia lungo circa sei volte l'elemento finito.
•Inserimento della combinazione "quasi permanente", atta a descrivere i carichi concomitanti al sisma, se non presente.
•Definizione degli spettri di risposta (sino a 5) per le analisi di pushover desiderate, ed in corrispondenza con gli stati limite desiderati. Gli spettri di risposta saranno identificati con etichette di tre lettere come "SLV", "SLC", "EA1", eccetera.
•Definizione delle zone dissipative (estremi di elementi trave o biella), mediante il comando Struttura-Aggiungi DZONA.
•Esecuzione della analisi modale sul modello padre.
•Scelta delle impostazioni delle analisi non lineari, in particolar modo per scegliere che tipo di non linearità attivare: solo di materiale, solo geometrica, o di materiale e geometrica. E' anche possibile sceglere le tolleranze e in generale varie impostazioni specifiche per le analisi non lineari.
Impostazione delle analisi di pushover
Una volta preparato il modello padre, ed eseguita la analisi modale su di esso, è possibile impostare le analisi di pushover. Ciò si fa con il comando Post-Pushover-Imposta, il quale dà accesso ad un dialogo che consente di impostare le pushover per ogni famiglia di spettri: ad esempio per SLV, SLC, SLO ed SLD. Le impostazioni della analisi non lineare propriamente detta si fanno invece altrove, nelle impostazioni del solutore CURAN.
Date le cinque famiglie di spettri (normalmente associate a stati limite diversi), si può scegliere per quali di esse attivare la richiesta di analisi di pushover e si può scegliere come impostare tali analisi di pushover.
Sono possibili due strategie alternative:
1.Attivare ed impostare le pushover per spettri diversi, associati a stati limite diversi. Ad esempio con le norme italiane per SLD ed SLV, o per SLO, SLD, SLV ed SLC.
2.Attivare ed impostare più spettri identici relativi allo stesso stato limite (ad esempio LV1, LV2...) ma usando modi diversi. Ciò consente, come vedremo, di eseguire una MPA (modal pushover analysis, ovvero una analisi pushover multimodale). Possono essere richiesti sino a 5 modi diversi.
Scelta una famiglia di spettri (ad esempio SLV) si devono impostare le sue analisi pushover. Ciò si fa specificando:
1.Il numero del nodo di controllo.
2.Il numero della combinazione che corrisponde ai carichi quasi permanenti.
3.Il numero di modo per la pushover in direzione X.
4.Il numero di modo per la pushover in direzione Y.
5.Il fattore di amplificazione delle azioni spettrali per la direzione X. Un fattore unitario applica lo spettro elastico con smorzamento al 5%.
6.Il fattore di amplificazione delle azioni spettrali per la direzione Y. Un fattore unitario applica lo spettro elastico con smorzamento al 5%.
7.Se per l'equivalenza che tara le proprietà dell'oscillatore semplice usare il metodo dell'Eurocodice 8 o quello delle NTC 2008/2018.
8.I livelli di prestazione richiesti per quello stato limite. Ovvero: le rotazioni rispetto alla corda nelle cerniere plastiche (elementi trave), i limiti di deformazione in trazione e compressione (elementi biella), e i limiti di drift.
Per definire quali elementi e nodi dovranno essere monitorati ai fini delle analisi di capacità, Sargon usa la seguente convenzione:
•Verranno monitorati gli elementi beam (trave) dichiarati dissipativi mediante il comando Struttura-Gerarchia-Aggiungi DZona
•Verranno monitorati gli elementi truss (biella) dichiarati dissipativi mediante il comando Struttura-Gerarchia-Aggiungi DZona
•Verranno memorizzati e monitorati i nodi selezionati al momento della esecuzione del comando e esplicitamente importati come estremi di drift da considerare all'interno del comando stesso. Quindi, prima di eseguire il comando di impostazione della pushover, è opportuno selezionare i nodi che corrispondono ai drift ai quali si è interessati.
Modelli padre e figli
Una volta avuta la disponibilità del modello padre, e impostate le pushover, Sargon può generare automaticamente molti modelli "figlio", che hanno le seguenti caratteristiche:
1.Hanno un primo caso di carico che corrisponde a un primo step non lineare, nel quale sono applicati i carichi quasi permanenti definiti dalla combinazione del modello padre. I modelli figlio assumono che tutti i casi di carico che definiscono la combinazione "quasi permanente" agiscano contemporaneamente ed esplicitamente come azioni (e non più come combinazioni), scalate al valore di combinazione definito nel modello padre.
2.Hanno un secondo caso di carico la cui piena applicazione corrisponderebbe alla assegnazione delle forze coerenti con il modo scelto (secondo il profilo di carico scelto), amplificate per la quantità predeterminata dall'utente (forze della pushover). Un fattore 1 corrisponde alle azioni spettrali relative allo spettro elastico (q=1, smorzamento del 5%).
3.Sono pronti per la esecuzione di una analisi non lineare, in cui sono attivate le stazioni. Quindi prima sarà applicato il primo caso di carico corrispondente ai carichi quasi permanenti, e poi da lì il secondo corrispondente alle analisi di spinta.
4.Sono tali da consentire la memorizzazione su disco di tutte le curve carico spostamento o carico deformazione necessarie a ricostruire i valori della "domanda" al crescere del carico.
5.Sono preimpostati in modo da usare l'arc length come metodo di analisi, in modo da procedere lungo eventuali rami discendenti o piatti.
Creazione dei modelli per le pushover e loro esecuzione
Dato un modello padre chiamato MODELLO, un certo spettro, ad esempio SLV, mediante in comando Post-Pushover-Crea Modelli! Sargon crea i seguenti modelli:
MODELLO_SLV_PUSHOVER_PX_MODAL.WSR Direzione X positiva, distribuzione modale.
MODELLO_SLV_PUSHOVER_MX_MODAL.WSR Direzione X negativa, distribuzione modale.
MODELLO_SLV_PUSHOVER_PX_CONSTANT.WSR Direzione X positiva, distribuzione costante.
MODELLO_SLV_PUSHOVER_MX_CONSTANT.WSR Direzione X negativa, distribuzione costante.
MODELLO_SLV_PUSHOVER_PY_MODAL.WSR Direzione Y positiva, distribuzione modale.
MODELLO_SLV_PUSHOVER_MY_MODAL.WSR Direzione Y negativa, distribuzione modale.
MODELLO_SLV_PUSHOVER_PY_CONSTANT.WSR Direzione Y positiva, distribuzione costante.
MODELLO_SLV_PUSHOVER_MY_CONSTANT.WSR Direzione Y negativa, distribuzione costante.
La esecuzione di tutte le analisi non lineari corrispondenti a tutti gli spettri richiesti, viene eseguita automaticamente mediante il comando Post-Pushover-Analizzali!.
Esame delle singole analisi di pushover

Una volta lanciate le analisi di pushover, sarebbe buona norma controllare i risultati della analisi per ciascuna di esse. Dato che il numero di queste analisi può essere molto elevato (sino a 40 in un sol colpo), è evidente che un tale lavoro può essere molto ingente. Comunque, se ci si limita ad una sola analisi per ciascuna direzione, verso e distribuzione di azioni, il numero di questi controlli scende a 2 per ciascuno stato limite con un massimo di 10 controlli totali.
Per controllare i risultati di una singola analisi occorre aprire il modello creato automaticamente ed eseguire il comando Post-Pushover-Prestazione. Questo comando non è accessibile sul modello padre, dato che non sarebbe chiaro a quale particolare pushover delle molte eseguite, esso si dovrebbe riferire.
Il comando corrisponde di fatto alla disponibilità del dialogo della figura precedente, ed alla disponibilità di un report come quello elencato qui di seguito (bottone Crea Report).
----------------------------------------------------
- -
- Pushover Results -
- -
- -
- Sargon © by Castalia srl - www.castaliaweb.com -
----------------------------------------------------
Model path: C:\ANALISI\SARGON\1190\Mensola.SLC.PUSHOVER_PX_MODAL.STATION_0002.pmc
Spectrum: SLC
Direction X
Orginal structure data
Period = 1.035 sec
Mode number = 1
Control node = 8
Combination = 1
Elastic spectrum force amplification factor= 3.000
Total applied shear (lambda = 1.) = 118775.163195 N
Partecipation mass = 35.10 ton
Conversion factor (Gamma) = 1.000
--------------------------------------------------
Method: NTC Norme Tecniche per le Costruzioni (N2)
--------------------------------------------------
Equivalent stiffness K,star = 1328.652672 N/ mm
Equivalent mass M,star = 35.100000 ton
Equivalent period T,star = 1.021 sec
Equivalent displacement at yield dy,star = 38.798575 mm
Equivalent force at yield Fy,star = 51549.830847 N
Equivalent ultimate displacement du,star = 98.205943 mm
Equivalent q factor q,star = 1.00
Equivalent mu factor mu,star = 1.00
Equivalent target displacement d,target,star= 30.198399 mm
Equivalent target force F,target,star= 40123.184173 N
Target displacement u,target = 30.198399 mm
Fraction of total applied shear lambda,target= 0.338
Di fatto è molto importante considerare la forma della curva SDOF carico spostamento (tasto F*-d*), per esaminare se l'analisi è stata spinta a sufficienza, e per verificare già a colpo d'occhio se la risposta è duttile o no.
I risultati sono dati in due piani: piano ADRS e piano F*-d*.
In quest'ultimo piano si dà sia la curva SDOF carico spostamento, sia la sua linearizzazione.
Nel piano ADRS (acceleration-displacement response spectrum), si danno le accelerazioni in funzione degli spostamenti. Lo spettro di risposta in accelerazione Sa(T) e in spostamento Sd(T) possono essere messi in relazione eliminando T dando luogo allo spettro ADRS, dove Sa è funzione di Sd: Sa(Sd).
La curva carico spostamento dell'oscillatore SDOF, dividendo le ordinate (forza) per la massa equivalente M* può anch'esso dar luogo a una curva accelerazione-spostamento (curva rossa), che viene rappresentata nel medesimo piano.
Il punto di intersezione tra le due curve rappresenta il performance point.
Considerando quindi il piano ADRS, ovvero accelerazione-spostamento, è possibile osservare se l'intersezione della curva di capacità (curva rossa) con quella di domanda (curva nera) avviene nel ramo elastico o in quello plastico dell'oscillatore semplice equivalente. Il punto di intersezione è il performance point, e lo spostamento del sistema SDOF corrispondente è il punto della analisi non lineare che corrisponde allo stato di deformazione della struttura originaria al quale si è interessati. In tutte le curve di risposta in funzione del parametro di carico, in corrispondenza a quel punto sarà possibile leggere il valore corrispondente e così stimare le domande per le rotazioni delle cerniere e per le elongazioni o accorciamenti delle bielle, così come per i drift di piano.
Tale ricerca, comunque, sarebbe molto laboriosa, e un comando specifico consente di automatizzarla per tutte le analisi di pushover e per tutti gli indicatori di cimento.
Possono avvenire alcune situazioni particolari:
•Il punto di intersezione è nel ramo elastico della curva rossa. Ciò implica che non vi è escursione plastica (vedi figura precedente).
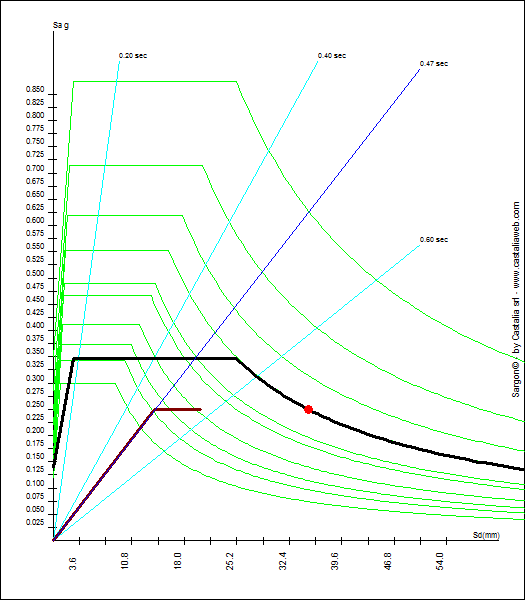
•il performance point sia al di là di quanto effettivamente calcolato con la analisi non lineare. In tal caso, o si deve aumentare l'entità della amplificazione (se l'analisi in arc length si è arrestata per il raggiungimento della lunghezza di arco richiesta), o si deve constatare che la struttura non è in grado di arrivare al performance point (ottenuto intersecando la estrapolazione della curva bilineare equivalente: ciò avviene per il raggiungimento di rotture o per la impossibilità di convergere, eventualmente anche a causa di fenomeni del secondo ordine, se attivati). In questo caso nel report sarà detto:
*** Target displacement higher than ultimate displacement!! ***
Verifica delle capacità
Lo scopo finale delle analisi di pushover è verificare che localmente la domanda di spostamento non ecceda la capacità. Ad una singola analisi di pushover possono essere associate dozzine di diversi indicatori da controllare, ad ognuno dei quali è associata una distinta curva in funzione del parametro di carico.

Se si considera per esempio un singolo indicatore, come può essere la rotazione plastica in una cerniera, si vede che occorrerebbe aprire la curva corrispondente (con il comando Post-Curve) alla stazione 2, elemento beam corrispondente, e verificare il punto corrispondente al performance point ad esempio della rotazione 2. Una delle operazioni compiute dal programma quando si esegue una pushover, è quella di aprire i file .pmc con le curve ed aggiungere a tutte queste curve memorizzate su file il punto corrispondente al performance point. Tale punto viene aggiunto e selezionato, e così appare in rosso aprendo la curva. E' da notare che l'ascissa è maggiore di 1 dato che siamo nella stazione 2, che va da 1 a 2, applicata al termine della stazione 1 che va da 0 ad 1 (nella figura che precede il performance point è 1.34-2.57mRad, dunque corrisponde a 0.34 volte la applicazione dei carichi della stazione 2).
Una tale operazione, da ripetersi per ogni indicatore e per ogni pushover sarebbe alquanto onerosa.
Quindi, a tale fine, è possibile adoperare il comando Post-Pushover-Risultati, che essenzialmente fa questa operazione in modo automatico:
•Per tutte le analisi di pushover richieste.
•Per tutti gli indicatori di danno richiesti.

Il comando è accessibile solo dal modello padre.
Alla esecuzione del comando compare il dialogo della figura precedente, che unifica la rappresentazione delle verifiche di danno.
1.I controlli posti a sinistra consentono di aggiungere o rimuovere dai risultati rappresentati in figura sismi (stati limite), direzioni (X o Y), Distribuzioni (costante o modale) e Segni (positivo o negativo).
2.Il piano è diviso in 4 quadranti, tre dei quali sono associati a famiglie di indicatori di danno. Il primo quadrante è associato alle rotazioni delle cerniere plastiche. Il secondo quadrante alle deformazioni delle bielle. Il terzo quadrante ai drift di piano. Il quarto quadrante è al momento inutilizzato.
3.La distanza dal centro (lunghezza del raggio) dà la misura dello sfruttamento, espresso come rapporto tra la domanda (calcolata dalla pushover) e la capacità (impostata dall'utente per le varie tipologie di danno). Circonferenze iso sfruttamento aiutano a capire la entità dei danneggiamenti.
4.Il colore dei simboli è in relazione con la entità dello sfruttamento, come ricordato dalla legenda.
5.La forma del simbolo, è in relazione con lo stato limite/sisma.
6.Tanto più i punti sono vicini al centro tanto meglio l'analisi.
7.Dato che le soglie (capacità) dipendono dallo stato limite (e crescono con gli stati limite più severi) non è in generale detto che le verifiche più severe siano quelle corrispondenti agli stati limiti annessi a sismi con scuotimenti maggiori.
Questa rappresentazione consente a colpo d'occhio di tenere sotto controllo molte decine di indicatori di danno, e dà una chiara idea della severità del cimento. La possibilità di isolare singoli stati limite, direzioni, distribuzioni e segni, consente di specializzare le rappresentazioni selettivamente. Il pulsante Crea Report dà luogo alla creazione di un file, in cui le quantità sono puntualmente indicate. Di seguito un esempio di tale file.
----------------------------------------------------
- -
- Target vs Capacity Pushover Results -
- -
- -
- Sargon © by Castalia srl - www.castaliaweb.com -
----------------------------------------------------
Model path: C:\ANALISI\SARGON\1190\Mensola.
------------
Caption
------------
C: capacity
const: constant
Dir: direction
F: force distribution
mod: modal
T: target
U: utilization ratio
V: verse of the applied forces (positive or negative)
----------------------------------------------------------------
SLV Dir:X F= mod V=+
SLV Dir:X F= mod V=+ Beam 1, axis 2 Rotation (rad) T= 2.049e-003 C= 2.014e-002 U=0.10
SLV Dir:X F= mod V=+ Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= mod V=+ Beam 3, axis 2 Rotation (rad) T= 1.833e-003 C= 2.014e-002 U=0.09
SLV Dir:X F= mod V=+ Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= const V=+
SLV Dir:X F= const V=+ Beam 1, axis 2 Rotation (rad) T= 2.049e-003 C= 2.014e-002 U=0.10
SLV Dir:X F= const V=+ Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= const V=+ Beam 3, axis 2 Rotation (rad) T= 1.833e-003 C= 2.014e-002 U=0.09
SLV Dir:X F= const V=+ Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= mod V=-
SLV Dir:X F= mod V=- Beam 1, axis 2 Rotation (rad) T=-2.049e-003 C= 2.014e-002 U=0.10
SLV Dir:X F= mod V=- Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= mod V=- Beam 3, axis 2 Rotation (rad) T=-1.833e-003 C= 2.014e-002 U=0.09
SLV Dir:X F= mod V=- Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= const V=-
SLV Dir:X F= const V=- Beam 1, axis 2 Rotation (rad) T=-2.049e-003 C= 2.014e-002 U=0.10
SLV Dir:X F= const V=- Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLV Dir:X F= const V=- Beam 3, axis 2 Rotation (rad) T=-1.833e-003 C= 2.014e-002 U=0.09
SLV Dir:X F= const V=- Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.014e-002 U=0.00
SLC Dir:X F= mod V=+
SLC Dir:X F= mod V=+ Beam 1, axis 2 Rotation (rad) T= 2.869e-003 C= 2.686e-002 U=0.11
SLC Dir:X F= mod V=+ Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= mod V=+ Beam 3, axis 2 Rotation (rad) T= 2.567e-003 C= 2.686e-002 U=0.10
SLC Dir:X F= mod V=+ Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= const V=+
SLC Dir:X F= const V=+ Beam 1, axis 2 Rotation (rad) T= 2.869e-003 C= 2.686e-002 U=0.11
SLC Dir:X F= const V=+ Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= const V=+ Beam 3, axis 2 Rotation (rad) T= 2.567e-003 C= 2.686e-002 U=0.10
SLC Dir:X F= const V=+ Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= mod V=-
SLC Dir:X F= mod V=- Beam 1, axis 2 Rotation (rad) T=-2.869e-003 C= 2.686e-002 U=0.11
SLC Dir:X F= mod V=- Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= mod V=- Beam 3, axis 2 Rotation (rad) T=-2.567e-003 C= 2.686e-002 U=0.10
SLC Dir:X F= mod V=- Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= const V=-
SLC Dir:X F= const V=- Beam 1, axis 2 Rotation (rad) T=-2.869e-003 C= 2.686e-002 U=0.11
SLC Dir:X F= const V=- Beam 1, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
SLC Dir:X F= const V=- Beam 3, axis 2 Rotation (rad) T=-2.567e-003 C= 2.686e-002 U=0.10
SLC Dir:X F= const V=- Beam 3, axis 3 Rotation (rad) T= 0.000e+000 C= 2.686e-002 U=0.00
Osservazioni sugli indicatori di danno
Al momento in Sargon sono disponibili tre famiglie di indicatori di danno: le rotazioni plastiche, le deformazioni degli elementi biella e i drift. Nel seguito saranno date alcune spiegazioni in merito a questi indicatori.
Rotazioni plastiche
In fase di assegnazione delle capacità viene richiesto un numero puro, pari al rapporto tra la "rotazione della corda" e la "rotazione della corda allo snervamento".
La rotazione della corda allo snervamento può essere valutata con la formula
![]()
dove My è il momento allo snervamento, L la "luce di taglio", E il modulo di elasticità e J il momento di inerzia (nel piano di flessione considerato). La "luce di taglio" è definita come M/V, dove M è il momento applicato e V il taglio. Alcune fonti la definiscono più precisamente come lunghezza del moncone di trave sino ad arrivare al punto di momento nullo. Ma allora L=M/V è una relazione in realtà assai discutibile, dato che viene trascurato l'effetto dei carichi trasversali. Comunque, di solito tale lunghezza non è molto dissimile da LM/2, dove LM è la lunghezza dell'elemento strutturale. Pertanto si può scrivere che grosso modo (precisioni molto elevate sono comunque prive di senso):
![]()
Dato che Sargon non utilizza un modello a plasticità concentrata, ma un modello a plasticità distribuita, la lunghezza degli elementi finiti non è più in relazione con la lunghezza degli elementi costruttivi originari. Ciò che viene memorizzato, è la rotazione plastica dell'intero elemento, ovvero l'integrale della curvatura plastica sulla lunghezza dell'elemento finito Le. Assumendo che la lunghezza dell'elemento Le sia intorno a LM/6 (il che implica aver diviso per 6 l'elemento originario nella fase di preparazione del modello), si può ottenere
![]()
Tale formula è impiegata dal programma per valutare la rotazione rispetto alla corda elastica, ed utilizza solo la lunghezza dell'elemento finito Le. La rotazione rispetto alla corda plastica θp è data dalla rotazione plastica dell'elemento, ottenuta integrando la curvatura plastica (si suppone implicitamente che tutta la rotazione plastica sia all'interno dell'elemento considerato. Ciò implica che non sia opportuno discretizzare con elementi troppo piccoli. Se la lunghezza della cerniera plastica è 1 o 2 volte l'altezza della sezione e questa è circa (1/15-1/20) di LM, si ha che la plasticizzazione non dovrebbe essere superiore a LM/7.5-LM/10, quindi ben entro il limite di LM/6). Per quanto detto la divisione in 6 sottoelementi è la scelta di elezione nella trattazione della pushover in Sargon.
Se in generale è k il fattore che moltiplicato per la lunghezza di elemento finito dà la lunghezza dell'elemento costruttivo, allora la rotazione rispetto alla corda elastica sarebbe (k/6) volte quella calcolata dal programma con la formula precedente. Ciò implica che gli sfruttamenti debbano essere moltiplicati per (6/k), dato che la rotazione rispetto alla corda elastica è a denominatore dello sfruttamento. Quindi ad esempio se k=10, gli sfruttamenti andranno moltiplicati per 6/10 = 0.6, sempre nella ipotesi che la plasticizzazione non abbia invaso altri elementi oltre a quello considerato.
Ulteriori migliorie ed ampliamenti sono previsti nelle versioni successive.
In effetti, sarebbe molto più semplice e più logico riferirsi, nei modelli a plasticità diffusa, alla deformazione della fibra più snervata, un indice molto più fisicamente associato al comportamento del materiale. Tuttavia, la legge non ne fa menzione.
I valori attualmente suggeriti da Sargon per θp/θy sono:
SLD 1 (stato limite di danno norme europee)
SLV 6 (stato limite vita norme europee)
SLC 8 (stato limite collasso norme europee)
IO 1 (stato limite "immediate occupancy" norme USA)
LS 6 (stato limite "life safety" norme USA)
CP 8 (stato limite "collapse prevention" norme USA)
L'utente può scegliere valori differenti.
Deformazioni delle bielle
Per definire la capacità di questi elementi viene fornito il rapporto tra la deformazione di trazione ε e quella allo snervamento εy, e, per gli elementi compressi, il rapporto tra la deformazione di compressione e la deformazione che porterebbe l'elemento alla instabilità εc.
Mentre per la prima definizione non vi è problema, dato che
![]()
per la determinazione della deformazione corrispondente alla instabilità il programma deve usare delle opportune curve di stabilità, dato che il carico critico euleriano non sarebbe cautelativo. Detto Nc il massimo valore di compressione sostenibile sull'elemento (una biella) si ha (valore positivo)
![]()
Nella versione attualmente rilasciata, il programma valuta Nc mediante le curve di stabilità dell'Eurocodice 3 / NTC 2008 / NTC 2018. Mediante le seguenti assunzioni:
•La lunghezza di libera inflessione è determinata mediante i coefficienti di libera inflessione stabiliti dall'utente.
•Se la forma sezionale è un angolare semplice si usa la curva b.
•Se la forma sezionale è un tubo tondo o Rhs si usa la curva a.
•Se la forma sezionale è a doppio T laminato, allora: se h/b > 1.2 e tf < 40, la curva è la b. Se tf > 40 la curva è la c. Se h/b < 1.2 e tf < 100 curva c, se no curva d.
•Altrimenti la curva è la c.
I valori attualmente suggeriti da Sargon per ε/εy in trazione sono:
SLD 0.25 (stato limite di danno norme europee)
SLV 7 (stato limite vita norme europee)
SLC 9 (stato limite collasso norme europee)
IO 0.25 (stato limite "immediate occupancy" norme USA)
LS 7 (stato limite "life safety" norme USA)
CP 9 (stato limite "collapse prevention" norme USA)
I valori attualmente suggeriti da Sargon per ε/εc in compressione sono:
SLD 0.25 (stato limite di danno norme europee)
SLV 4 (stato limite vita norme europee)
SLC 6 (stato limite collasso norme europee)
IO 0.25 (stato limite "immediate occupancy" norme USA)
LS 5 (stato limite "life safety" norme USA)
CP 7 (stato limite "collapse prevention" norme USA)
L'utente può scegliere valori differenti.
Drift di piano
I drift sono definiti da coppie di nodi aventi la medesima asissa e ordinata. I nodi posti su uno stesso allineamento in pianta, e selezionati al momento della impostazione della pushover, vengono su richiesta dell'utente ordinati per quota crescente, e se n è il numero di nodi trovato su un allineamento in pianta, il numero di drift richiesti su quell'allineamento sarà (n-1).
La valutazione dei limiti dei drift di piano, dipende da una moltitudine di fattori, non ultima la tipologia strutturale. In letteratura si sono trovati valori assai dispersi.
I valori attualmente suggeriti da Sargon per i drift sono:
SLD 4/1000 (stato limite "di danno" norme europee)
SLV 25/1000 (stato limite "vita" norme europee)
SLC 50/1000 (stato limite "collasso" norme europee)
IO 4/1000 (stato limite "immediate occupancy" norme USA)
LS 25/1000 (stato limite "life safety" norme USA)
CP 50/1000 (stato limite "collapse prevention" norme USA)
E' opportuno segnalare la spiccata fiabesca convenzionalità delle etichette "danno", "vita", "collasso" assegnate a tali valori limite.
L'utente può scegliere valori differenti.