COME ESEGUIRE ANALISI NON LINEARI CON IL SOLUTORE CURAN (CURved ANalysis)
1 Generalità.
A partire dalla versione 9.60 tra i solutori di Sargon è disponibile anche il solutore denominato CURAN (CURved ANalysis). Questo solutore è in fase di sviluppo e sarà il solutore di Sargon per i problemi nonlineari, rimpiazzando gradualmente il solutore SOCLEVER. CURAN è capace di gestire sia la nonlinearità di materiale che quella geometrica (effetti del secondo ordine), che quella di contatto.
La versione LIGHT di CURAN è eseguibile senza costi aggiuntivi per chiunque disponga del solutore statico CLEVER. Questa versione include i soli elementi truss e molla come elementi non lineari, mentre tutti gli altri elementi sono trattati come elementi elastici lineari.
La versione FULL di CURAN, invece, come elementi nonlineari include bielle, travi (a fibre), membrane, piastre, solidi, molle e nodi semirigidi.
CURAN LIGHT |
CURAN FULL |
bielle |
bielle |
|
travi |
|
membrane |
|
piastre |
|
solidi |
molle
|
molle nodi semirigidi |
CURAN dispone di un solutore interno sparse matrix, lo stesso già ampiamente testato all’interno di CLEVER. Ciò rende la soluzione dei problemi non lineari rapida ed efficiente. CURAN supporta sia il metodo di Newton completo (riassemblaggio ad ogni iterazione) sia il metodo di Newton modificato (assemblaggio all’inizio di ogni step di carico).
2 Le nonlinearità gestite da CURAN
2.1 Generalità
CURAN può gestire indipendentemente o contemporaneamente tre tipi di nonlinearità: la nonlinearità di materiale, la nonlinearità geometrica, e la nonlinearità di contatto.
La nonlinearità di materiale serve a trattare elementi che abbiano una legge costitutiva in cui non vi è un legame lineare tra sforzi e deformazioni, o che presentano, nel monoassiale, dissimmetria di comportamento (no-tension e no-compression). Dato che CURAN dispone anche del controllo della soluzione per mezzo di arc-length, è anche possibile seguire il ramo di softening, ovvero il ramo a pendenza negativa del legame costitutivo. CURAN può seguire i cicli di carico e scarico ed il comportamento incrudente per quei materiali per i quali sia disponibile. In particolare, per i metalli CURAN dispone di leggi di incrudimento isotropo, cinematico e misto ed è in grado di seguire il comportamento ciclico. Per il calcestruzzo al momento attuale le due leggi disponibili (parabola-rettangolo e Kent e Park modificata) non includono ancora il comportamento ciclico, ma solo quello monotono, che però è sufficiente per la gran parte delle applicazioni pratiche. La nonlinearità di materiale, se applicata per mezzo di leggi costitutive che presentano un plateau, dà luogo, al crescere del carico, a situazioni in cui si formano dei meccanismi. CURAN è in grado di prevedere il valore del parametro di carico adimensionale λ che corrisponde alla formazione di tali meccanismi. Il numero delle leggi costitutive disponibili sarà via via ampliato.
La nonlinearità geometrica serve a studiare gli effetti del secondo ordine. Tutti gli elementi finiti ad eccezione della molla dispongono della loro matrice di rigidezza geometrica, i cui valori dipendono dalle sollecitazioni che via via si sviluppano negli elementi. Al crescere degli sforzi di compressione si ha un progressivo indebolimento e la matrice di rigidezza geometrica tende a diventare negativa. La somma della matrice di rigidezza del materiale (eventualmente anch'essa non lineare) e della matrice di rigidezza geometrica, costituisce la matrice di rigidezza complessiva. Se si lavora in controllo di forza, CURAN segnala il livello del carico a cui corrisponde la perdita della condizione di definizione positiva della matrice complessiva. Una tale condizione segnala il raggiungimento di un punto singolare, che può essere un punto limite o un punto critico. In altre parole, CURAN è in grado di valutare il livello del carico che corrisponde a un certo carico critico.
La nonlinearità di contatto è legata allo svilupparsi o allo svanire di forze reattive legate al contatto tra superfici che non si devono compenetrare. Questo tipo di nonlinearità è molto utile per studiare problemi di contatto monolatero tra superfici deformabili, per le quali la superficie di contatto finale sia incognita. Un importante campo di applicazione riguarda lo studio dei collegamenti delle strutture in acciaio (piastre di base, collegamenti flangiati). La nonlinearità di contatto comporta la "comparsa" e la "sparizione" di opportuni "elementi di contatto" che connettono i nodi di una superficie detta "contactor" (contatto), con gli elementi di un'altra superficie detta "target" (obiettivo). Da un punto di vista pratico la nonlinearità di contatto viene definita assegnando ad opportuni elementi piastra (a tre o quattro nodi e di tutti i tipi disponibili) un numero di "superficie contatto" o un "numero di superficie target".
Le tre nonlinearità possono essere attivate indipendentemente e quindi si possono avere questi tipi di analisi:
1.Nessuna nonlinearità
2.Solo NL di materiale.
3.Solo NL geometrica.
4.Solo NL di contatto.
5.NL di materiale e geometrica.
6.NL di materiale e di contatto.
7.NL geometrica e di contatto.
8.NL di materiale, geometrica e di contatto.
L'onere computazionale cresce al crescere del numero di nonlinearità attivate. L'analisi nonlineare è un calcolo specialistico e deve sempre essere condotta con attento giudizio esperto.
2.2 Nonlinearità di materiale
La nonlinearità di materiale è attivata assegnando agli elementi un materiale che presenti una qualche forma di nonlinearità, ovvero, che non sia indefinitamente elastico lineare. Se un elemento non riceve un materiale nonlineare, ma un materiale lineare, esso sarà trattato come elemento lineare per ciò che attiene alla nonlinearità di materiale.
Le leggi costitutive disponibili sono le seguenti:
•Indefinitamente elastico
•Elastico fragile
•Elastico non lineare
•Ramberg-Osgood
•Elastico perfettamente plastico
•Rigido plastico
•Elasto-plastico bilineare, trilineare o per punti
•Parabola-rettangolo (carico monotono in controllo di carico o arc-length)
•Kent e Park modificata (carico monotono in controllo di carico o arc-length)
Inoltre, per i nodi semirigidi, è disponibile la legge Li-Shen.
Tutti i precedenti comportamenti possono essere simmetrici, oppure no tension oppure no compression. E’ inoltre possibile specificare le deformazioni ultime in trazione e/o compressione che corrispondono alla rottura e studiare le ridistribuzioni susseguenti alle rotture e/o lo svilupparsi di meccanismi (determinando il moltiplicatore limite).
Con CURAN LIGHT è possibile studiare problemi in cui le bielle (ad esempio i controventi) presentano comportamenti di questo tipo.
Gli elementi e le non linearità gestibili da CURAN FULL sono quindi:
-Bielle full reactive, no tension, no compression, con legge elastica lineare, bilineare, trilineare, elastica perfettamente plastica, rigido-plastica, Ramberg Osgood (elasticità non lineare), Parabola rettangolo e Kent e Park, e per le leggi plasticheadatte ai metalli incrudimento cinematico, isotropo e misto. Criterio di snervamento di Von Mises. Gap. Rottura del materiale per eccesso di deformazione.
-Molle traslazionali e rotazionali con analoga legge costitutiva (stesse tipologie bielle).
-Molle per semirigidezza di elementi beam con analoga legge costitutiva (e quindi anche semirigidezze bilineari, con gap, elastiche perfettamente plastiche, ecc.).
-Elementi membrana a 3 e 4 nodi con legge costitutiva elasto plastica plane stress e incrudimento cinematico, isotropo e misto. Vari tipi di ritorno su luogo plastico.
-Elementi piastra a 3 e 4 nodi (integrazione di Lobatto). Legge costitutiva elasto plastica e incrudimento cnematico, isotropo e misto.
-Elementi solidi (tetra, brick, penta) in campo elasto plastico (tensore a sei componenti). Incrudimento cinematico, isotropo e misto.
-Elementi beam non lineari con non linearità concentrata nelle molle semirigide (tutte le leggi costitutive valide per le molle). Viene gestita la rottura per eccesso di deformazione del giunto.
-Elementi beam non lineari per non linearità di materiale: modello beam a fibre. Viene gestita la rottura della fibra generica per eccesso di deformazione. La generica fibra segue la legge del materiale (tutti i tipi di leggi costitutive menzionate);In seguito saranno probabilmente aggiunte più sezioni (ad esempio le formate a freddo con opportune trattazioni, le sezioni in c.a. o fibro-rinforzate e le composte) e funzionalità.
-Elementi beam aventi sia la non linearità dei nodi semi rigidi sia la non linearità del materiale (per le forme sezionali gestire dai modelli a fibre).
2.2 Nonlinearità geometrica
La nonlinearità geometrica è studiata per mezzo dell'assemblaggio di opportune matrici di rigidezza geometrica per gli elementi. Gli elementi dotati di matrice di rigidezza gometrica sono:
1.Gli elementi biella.
2.Gli elementi trave.
3.Gli elementi trave con nodi semirigidi (formulazione particolare).
4.Gli elementi membrana a tre e quattro nodi.
5.Gli elementi piastra sottile e spessa a tre e quattro nodi.
6.Gli elementi solidi a 4, 6 ed 8 nodi.
Detto λ il parametro di carico il problema può essere descritto in generale in questo modo:
[K(λ)+KG(λ)] u=λp (1)
dove K(λ) è la parte della matrice di rigidezza associata al materiale ed al possibile contatto, mentre KG(λ) è la matrice di rigidezza geometrica. Nel caso di materiale elastico lineare, la parte della matrice associata al materiale è costante
K(λ)=KE
mentre nel caso di non linearità di materiale essa cambia in funzione della rigidezza via via diversa dei punti in cui lo sforzo è campionato. Nel semplice caso uniassiale, al diminuire del modulo elastico E delle fibre, o al suo modificarsi in seguito ad unloading, la matrice K muta. Se si fa l'ipotesi (non sempre verificata) che le azioni interne crescano linearmente col carico, e se il materiale è elastico lineare, allora il problema (1) si semplifica come segue
[K+λKG] u=λp
La condizione per cui
det(K+λKG)=0
individua in tal caso i carichi critici (analisi di buckling agli autovalori). E' evidente che il problema non lineare (1) è molto più generale, anche perché consente di studiare la interazione tra plasticità ed instabilità che è alla base degli approcci di legge. La disponibilità di elementi piastra non lineari sia per materiale che per effetti geometrici potrebbe consentire, ad esempio, di determinare il carico ultimo di elementi dei quali non siano disponibili adeguate curve di stabilità. CURAN, in altre parole, mette in condizione di svolgere analisi molto avanzate ed in linea con il corrente stato dell'arte.
2.3 Nonlinearità di contatto

(figura tratta da V. A. Yastrebov, Introduction to Computational Contact Mechanics, Centre des Materiaux, MINES, Paris Tech)
Date due superfici denominate contatto e obiettivo poste ad una certa distanza iniziale d, si può definire un tipo di nonlinearità, detta di contatto, nel modo che segue. Si consideri un generico nodo della superficie di contatto (in verde in figura). Se questo nodo dista dalla superficie obiettivo (i cui nodi sono in blu in figura) più di una certa soglia detta gap, g, il contatto non esiste. Se invece la distanza di questo generico nodo è inferiore a g, allora il contatto esiste e si sviluppano delle forze reattive, proporzionali a |d-g| tramite una costante di penalty K, che tendono ad allontanare il nodo della superficie di contatto dai nodi della superficie obiettivo. Non è necessario che i nodi della superficie di contatto corrispondano ai nodi della superficie obiettivo. Il brusco decadere a zero delle forze scambiate può dare luogo ad instabilità numerica. Per questo motivo CURAN implementa il metodo descritto nel testo di Crisfield, che associa una curva esponenziale atta a riscalare i valori di rigidezza (che altrimenti passerebbero da K a 0 e da 0 a K). Si tratta del metodo descritto nel volume Advanced Topics, e dovuto a Zavarise. In pratica si ha
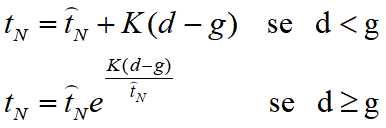
dove:
•tN indica la forza normale scambiata tra il nodo della superficie di contatto e i nodi della superficie obiettivo (questa forza si ripartisce sui nodi obiettivo in misura dipendente dalla loro posizione, i nodi obietivo sono i tre o quattro nodi di un elemento prescelto come target tra quelli della superficie target);
•d è la distanza tra le superfici, che varia nel corso della analisi al progredire della deformazione e della applicazione delle forze;
•g è il gap preimpostato;
•K è una costante di penalty (ha le dimensioni di una rigidezza traslazionale, forza diviso spostamento);
•il termine tN con soprassegno è una costante negativa che ha la unità di misura di una forza.
Con questa formulazione, che stabilizza di molto il problema da un punto di vista numerico, le superfici si scambiano delle forze anche quando il gap è aperto, anche se tali forze decrescono molto rapidamente (esponenzialmente) a zero.
Da un punto di vista sostanziale, la nonlinearità di contatto corrisponde alla generazione automatica di tanti elementi di contatto fittizi (grosso modo in giallo in figura), la cui rigidezza cambia in funzione della deformazione, un po' come si fosse una qualche "deformazione" atta a mutare la rigidezza.
La nonlinearità di contatto può comportare un onere computazionale molto forte. E' bene adottare strategie di soluzione che comportino incrementi di carico modesti, in specie nella fase iniziale, quando la superficie di contatto è incognita e deve essere determinata con le iterazioni.
I risultati di una analisi di questo tipo possono essere controllati con il comando Post-Reazioni Vincolari-Mostra. Infatti, le reazioni scambiate tra i nodi vengono salvate dal solutore sotto forma di residui e quindi possono essere visualizzate come reazioni vincolari. A causa della adozione del metodo di Zavarise, è possibile che forze di trazione molto piccole siano presenti nella soluzione finale. La loro presenza, se, come dovrebbe data la legge adottata, si tratta di forze molto molto piccole, non inficia la bontà della soluzione.
Nella figura successiva si vede il risultato di una analisi con nonlinearità di contatto relativa a una piastra di base.

L'elemento è inflesso e lungo la flangia compressa si sviluppano forze locali di contatto. Intorno alle zone dove sono presenti dei tirafondi tesi si sviluppano delle forze di contatto (effetto leva) dovute alla controflessione della piastra di base indotta dal tiro dei bulloni.
Nel caso di compressione semplice (figura successiva), dato che la piastra è abbastanza sottile, si sviluppano delle forze di contatto in una regione (superficie di contrasto) tutta intorno alla impronta della colonna, che ricalca da vicino quella proposta da Eurocodice 3 parte 1.8.

3 File gestiti da CURAN
Curan gestisce i seguenti file:
.CUI file di input formattato
.COG file LOG con i messaggi nel corso della esecuzione
.COU file ASCII di output
.SDB file binario di output (sforzi)
.DDB file binario di output (spostamenti)
.RDB file binario di output (reazioni vincolari)
.FDB file binario con i risultati delle fibre (elementi beam a fibre)
.PMC file binario conenente le curve richieste prima dell'analisi
.TEMPX file temporanei che possono essere eliminati
Tutti questi file sono creati automaticamente. Per le successive operazioni di post processing sono necessari i soli file .SDB, .DDB, .RDB e .PMC.
Nella descrizione del funzionamento di CURAN si fa uso di una terminologia che deve essere ben compresa. In questa sezione si danno alcune importanti definizioni.
Caso di carico: un insieme di forze che vengono applicate contemporaneamente in modo gradualmente crescente da 0 ad 1, e che vengono applicate alla struttura a partire da una situazione di sforzi e spostamenti nulli. La presenza di più casi di carico non costituisce un load path.
Stazione di carico (load station): un insieme di forze che vengono applicate contemporaneamente in modo gradualmente crescente con intensità scalata da 0 ad 1, e che vengono applicate sulla struttura a partire da una situazione di spostamenti e sforzi non nulli, ottenuti in generale da una stazione di carico precedente. La successione di più stazioni di carico costituisce un load path.
Passo di carico (load step): nella applicazione di un caso di carico o di una stazione di carico un load step costituisce l’applicazione di un incremento di carico di intensità scalata compresa tra 0 ed 1, ed atto ad aggiungersi a precedenti passi di carico, con il fine di raggiungere il pieno completamento del caso di carico o della stazione di carico, ovvero il raggiungimento della intensità completa e scalata di 1.
Dimensione del passo di carico (step size): è un numero compreso tra 0 ed 1. Se la dimensione del passo di carico è prefissata essa è eguale a 1/nstep, dove nstep è il desiderato numero di passi di carico. Se la dimensione del passo di carico è invece determinata automaticamente, allora la dimensione del passo di carico è inizialmente pari a 1/nstep e viene poi adeguata nel corso dell’analisi in funzione del grado di nonlinearità riscontrata.
Iterazione: l’applicazione di uno step di carico avviene mediante un procedimento iterativo. In ogni iterazione vengono calcolate le forze interne e i residui e la norma dell’indice di errore (sia essa la variazione di spostamento o le forze non equilibrate) viene raffrontata con una opportuna misura di errore.
Norma dell’errore: dato un vettore indice di errore la sua norma può essere di due tipi. A) La SRSS, radice quadrata della somma dei quadrati. B) Il massimo valore in modulo dei termini del vettore. Come vettore dei indice di errore si può prendere, in generale: A) il vettore delle forze non equilibrate da applicare alla iterazione successiva; B) il vettore degli spostamenti aggiuntivi della ultima iterazione; C) il lavoro fatto dal vettore delle forze applicate all’ultima iterazione per la variazione di spostamento della ultima iterazione.
Punto limite: se nel corso della applicazione dei carichi la struttura arriva in qualche parte ad essere un meccanismo ciò viene segnalato e la elaborazione si arresta. Il livello del moltiplicatore dei carichi (del caso di carico o della stazione di carico corrente) compreso tra 0 ed 1 a cui corrisponde il punto limite viene stampato. L’elaborazione prosegue con il caso di carico successivo. Nel caso di carico in cui si ha un meccanismo, restano forze non equilibrate dato che viene scritto il quadro di spostamenti, deformazioni e sforzi corrispondente al punto immediatamente precedente il punto limite.
Moltiplicatore dei carichi: è un numero adimensionale compreso tra 0 (all’inizio del caso di carico o della stazione di carico) ed 1 (alla fine).
Strategia di analisi: CURAN prevede attualmente il metodo di Newton completo ed il metodo di Newton modificato.
Arc-length: è un metodo di analisi che consente di seguire il ramo softening di una struttura, ovvero incrementi di spostamento a cui corrispondono decrementi di carico. Si può chiedere il passaggio automatico dal controllo di forza al controllo di arc-length una volta che siano verificate certe condizioni.
5 Strategie di lavoro con CURAN
CURAN può essere usato in vari modi, al fine di ottenere varie informazioni. Le note seguenti si riferiscono alla versione attualmente rilasciata.
Due sono le possibili strategie di analisi usando CURAN: la prima consiste nell’esaminare tutte le combinazioni di carico come “casi di carico” a sé stanti ripartendo ogni volta da zero; la seconda strategia di analisi consiste nel seguire la struttura lungo un load path, costituito dalla successione di un opportuno numero di stazioni di carico.
Come è noto in ambito non lineare non vale il principio di sovrapposizione degli effetti, quindi la risposta della struttura dipende dalla successione con cui sono applicati i carichi A+B può dare risultati diversi da B+A. In teoria se si devono esaminare n combinazioni di carico bisognerebbe esaminare, per ognuna delle combinazioni, un certo numero di percorsi di carico. Ciò porterebbe a un onere computazione molto forte e quindi di solito non si fa. La norma stessa consente di applicare tutte le azioni che compongono una certa combinazione, contemporaneamente e scalando l’aggregato da 0 ad 1. Ciò consente di trattare ogni combinazione di carico del modello lineare come un “caso di carico” nel modello non lineare.
E’ tuttavia anche possibile esaminare la successione degli effetti che si creano applicando le azioni in modo da assegnare prima i carichi associati a una causa fisica, poi le azioni associate a un’altra causa fisica, e così via.
Per chiarire le idee supponiamo per semplicità di aver esaminato un modello lineare con tre casi di carico G, Q, W e ad esempio solo quattro combinazioni:
1,4G+1,5Q+1,05W
1,4G+1,05Q+1,5W
1G+1,5W
G+1,5Q
Fatta l’analisi lineare (che sfrutta il principio di sovrapposizione degli effetti) potremo desiderare di fare un’analisi non lineare. Se decidiamo di avvalerci della possibilità di normativa di aggregare G,Q e W e farli crescere assieme, potremo operare nel seguente modo:
a)Salviamo il modello lineare con un altro nome
b)Con il comando Edit-Casi-Combina generiamo una situazione in cui ci sono 4 casi di carico già con le azioni G, Q, W combinate in modo giusto.
c)Eseguiamo un’analisi non lineare con CURAN sui quattro “casi di carico” combinati (essi corrispondono in realtà alle combinazioni del modello lineare).
Se invece vogliamo studiare il problema della successione dei carichi seguendo il load path relativo alla combinazione 2, allora possiamo fare così:
a)Salviamo il modello lineare con un altro nome
b)Cancelliamo tutte le combinazioni
c)Aggiungiamo tre nuove combinazioni così fatte:
1.1,4G
2.1,05Q
3.1,5W
d)Con il comando Edit-Casi-Combina generiamo automaticamente a partire dalle combinazioni una situazione in cui il load path della combinazione 2 è schematizzato con tre load station: nella prima si mette il permanente per 1,4; nella seconda il variabile per 1,05; nella terza il vento per 1,5.
e)Eseguiamo CURAN chiedendo che venga eseguito un load path.
E’ da notare che i load path possibili per la combinazione 2 sono in teoria infiniti: nessuno sa in che modo i carichi si succederanno sulla struttura. Un’ ipotesi che di solito si fa è quella di applicare prima i permanenti, poi i variabili di lunga durata ed infine i variabili di breve durata, come abbiamo fatto.
Comandi utili all’uso di CURAN
I comandi utili all’uso di CURAN sono i seguenti:
Questo comando consente di aggiungere un materiale specificandone anche le proprietà non lineari. Tra i materiali di archivio sono stati aggiunti materiali PP (perfettamente plastici), EP2 (elasto plastici bilineari), NC (no compression) e NT (no tension). Se il materiale non è presente in archivio (come è probabile dato che ad un materiale lineare corrispondono decine di possibili modelli costitutivi non lineari) è possibile aggiungerlo ex novo, avendo cura di usare un nome univoco.
Edit-Proprietà-Modifica materiale
Si può usare questo comando per modificare le proprietà di un materiale non lineare precedentemente introdotto, così sperimentando varie possibilità.
Edit-Vincoli-Svincoli delle travi
Questo comando consente di assegnare nodi semirigidi nonlineare agli estremi degli elementi beam.
Edit-Proprietà-Aggiungi semirigidezza
Questo comando consente di aggiungere una semirigidezza che potrà essere assegnata ai nodi semirigidi.
Edit-Proprietà-Modifica semirigidezza
Questo comando consente di modificare una semirigidezza tra quelle definite nel modello.
Questo comando serve a bypassare il problema della mancata validità del principio di sovrapposizione degli effetti. Nei paragrafi precedenti abbiamo visto due esempi di uso di questo comando.
Con questo comando si imposta il funzionamento di CURAN e lo si lancia.
6 Le impostazioni di funzionamento di CURAN

Informazioni dettagliate saranno date nella spiegazione del dialogo per la impostazione dell'analisi non lineare.
Il flag Attiva stazioni decide che tipo di funzionamento dare al solutore, ovvero se farlo funzionare a casi di carico o a stazioni. I risultati ottenuti saranno ovviamente completamente diversi.
Degli altri parametri si è accennato brevemente. Qui si vuole dare qualche ulteriore ragguaglio su alcuni di essi.
Nel controllo automatizzato della ampiezza del passo, si usa un esponente compreso tra 0,5 ed 1. La formula (si veda il Crisfield, Nonlinear Finite Element Analysis for Solid and Structures, Wiley) è la seguente:
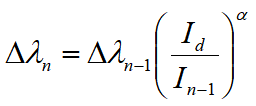
dove Id è il numero desiderato di iterazioni, In-1 è il numero di iterazioni al passo precedente, α è l'esponente di cui si sta parlando e Δλ è l'incremento di carico adimensionale.
Il valore così calcolato di incremento ha poi un massimo e un minimo che non possono essere superati, dati dai valori Massimo incremento e Minimo incremento.
Se non si ha la certezza che venga attivata una significativa nonlinearità si può lasciare come numero di passi di carico per ogni stazione il numero 1. Semmai tale numero potrà essere ridotto ove si verifichi una certa difficoltà di convergenza. Analogamente l'entità della norma dell'errore ed il numero di tali norme, dovrebbe essere deciso in funzione della severità del problema allo studio.
7 Le leggi costitutive supportate da CURAN.
Deformazioni ultime
Tutte le leggi costitutive utilizzano le deformazioni ultime positiva epsup e negativa epsum. Nel caso in cui il materiale sia elastico lineare, esso trova comunque un limite nel raggiungimento delle deformazioni ultime: se queste vengono raggiunte il materiale “si rompe” la tensione precipita a zero e l’elemento non reagisce più (se si tratta del punto di Gauss di un elemento, è questo ad essere inattivato). Pertanto la simulazione di un materiale elastico indefinitamente elastico deve essere ottenuta mediante la impostazione di elevate deformazioni di rottura. Il valore proposto è 0,02, corrispondente a 210000x0,02=4200MPa per un acciaio normale. Se il materiale è plastico, il flusso plastico viene interrotto al raggiungimento della deformazione limite, innescando la rottura.
No tension- no compression
Tutte le leggi costitutive possono essere opzionalmente rese no tension o no compression. Se non viene raggiunta la deformazione ultima in caso di inversione del carico il materiale può ricominciare a reagire ove il segno della deformazione si inverta. Se invece viene raggiunta la deformazione ultima, allora anche un’eventuale inversione di segno lascia inalterato lo stato di rottura.
Indefinitamente elastica
L'indefinitamente è legato alla ampiezza delle deformazioni ultime.
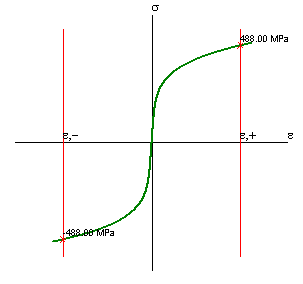
E=210000; K = 1000; n = 0.2; epsu = +/-0.03
La legge di Ramberg-Osgood è una legge di tipo elastico non lineare, quindi il materiale non dissipa. Essa è descritta dalla seguente equazione:
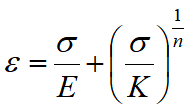
La formula del lavoro originario è lievemente diversa dalla precedente, anche se a questa si può ricondurre con un’ opportuna scelta dei parametri. Nel lavoro originario di Ramberg-Osgood la formula è:
![]()
Il legame tra i parametri nelle due formulazioni è il seguente:
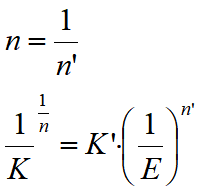
Dalla seconda delle quali si ottiene, elevando ambo i membri alla n, facendo il reciproco di ambo i membri
![]()
Nel caso in cui vi sia solo loading, la legge di Ramberg-Osgood può anche essere utilizzata per simulare situazioni elasto plastiche, dato che la nonlinearità del suo andamento può simulare leggi elasto plastiche in fase di loading.
Elastica-perfettamente plastica
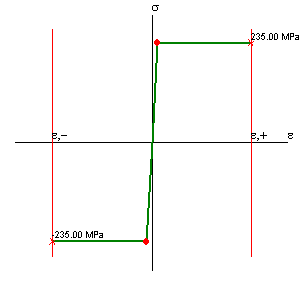
E=210000; σy=235MPa. epsu = +/- 0.02.
Questa legge è individuata dai seguenti parametri:
E modulo di elasticità in fase lineare
σy tensione di snervamento
ν coefficiente di Poisson
Il flusso plastico avviene senza incrudimento.
Rigida-perfettamente plastica
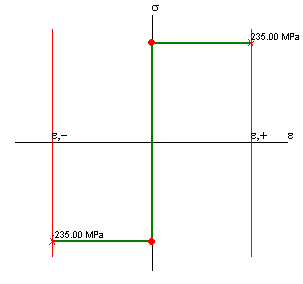
Questa legge è individuata dai seguenti parametri:
σy tensione di snervamento
ν coefficiente di Poisson
Numericamente la rigidezza infinita è simulata con E= 1.e12.
Elasto-plastica bilineare
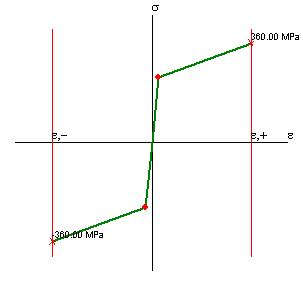
ε1=0.001119047; σ1=235; ε2=0.01678; σ2=360;
Questa legge è individuata dai seguenti parametri:
ν coefficiente di Poisson
ε1 deformazione allo snervamento
σ1 tensione allo snervamento
ε2 deformazione estrema
σ2 tensione corrispondente alla deformazione estrema
Non sono ammesse estrapolazioni, quindi è buona cosa far corrispondere la deformazione estrema con la deformazione ultima. Si assume che la legge – se non si è attivata l’opzione no tension o no compression – sia simmetrica.
Il tipo di incrudimento può essere isotropo, cinematico o misto.
Elasto-plastica trilineare

ε1=0.001119047; σ1=235; ε2=0.005; σ2=300; ε3=0.01678; σ3=360;
Questa legge è individuata dai seguenti parametri:
ν coefficiente di Poisson
ε1 deformazione allo snervamento
σ1 tensione allo snervamento
ε2 deformazione intermedia
σ2 tensione corrispondente alla deformazione intermedia
ε3 deformazione estrema
σ3 tensione corrispondente alla deformazione estrema
Non sono ammesse estrapolazioni, quindi è buona cosa far corrispondere la deformazione estrema con la deformazione ultima. Si assume che la legge – se non si è attivata l’opzione no tension o no compression – sia simmetrica.
Il tipo di incrudimento può essere isotropo, cinematico o misto.
Elasto-plastica per punti
In questo caso, oltre al coefficiente di Poisson, si danno tante coppie di valori (ε, σ) tanti sono i punti definiti. Deve sempre essere inclusa l’origine. I punti sono ordinati per deformazioni crescenti (prima le massime deformazioni negative, poi le negative, poi l’origine, poi le deformazioni positive, poi la massima deformazione positiva).
Non sono ammesse estrapolazioni, quindi è buona cosa far corrispondere la deformazione estrema (positiva e negativa) con la deformazione ultima.
Il tipo di incrudimento può essere isotropo, cinematico o misto.
Questa legge costitutiva serve per i nodi semirigidi ed è definita in [1]. Vanno forniti i seguenti parametri:
Ke initial stiffness
Kp hardening stiffness
fip rotazione corrispondente a Mp
Mp momento plastico

[1] Advanced Analysis and Design of Steel Frames, Guo-Quiang Li and Jin-Jun Li, Wiley, 2007.
•Parabola rettangolo (carico monotono)
Per la legge costitutiva di tipo parabola-rettangolo vanno forniti i seguenti parametri (tutti positivi, anche se per il programma le compressioni sono negative):
fc tensione limite di compressione del calcestruzzo
εc0 deformazione associata alla tensione limite
Et modulo elastico a trazione
ft tensione limite a trazione
ν coefficiente di Poisson

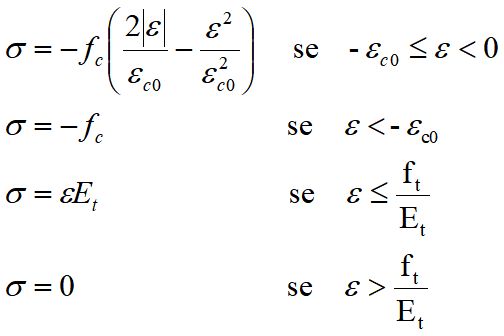
•Kent e Park modificato (carico monotono)
Per la legge costitutiva di Kent e Park modificata vanno forniti i seguenti parametri (tutti positivi, anche se per il programma le compressioni sono negative):
fc tensione limite di compressione del calcestruzzo
εc0 deformazione associata alla tensione limite
Z pendenza del ramo di softening
Et modulo elastico a trazione
ft tensione limite a trazione
ν coefficiente di Poisson

La legge di Kent e Park implementata prevede un residuo di resistenza pari a -0,2fc.
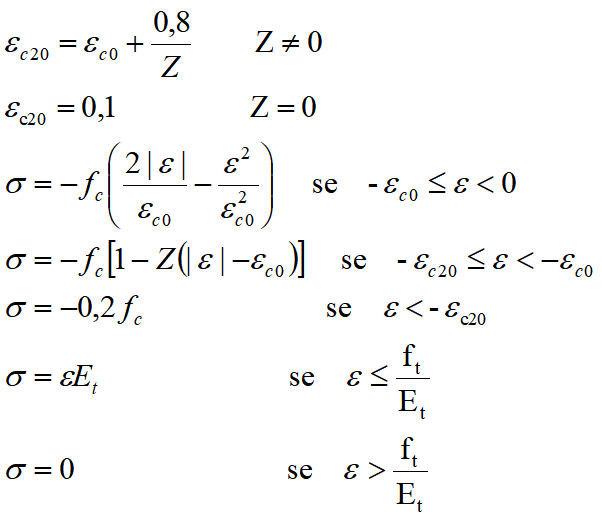
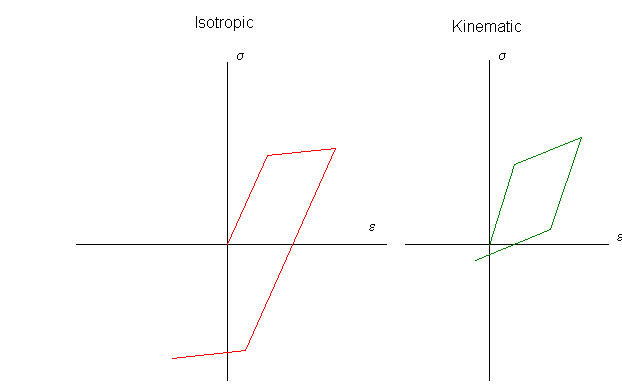
L’incrudimento è determinato dal parametro β che può assumere valori compresi tra 0 (incrudimento cinematico) ed 1 (incrudimento isotropo).
Nell’incrudimento isotropo un incrudimento al positivo comporta un analogo incrudimento al negativo. L’ampiezza della zona elastica va così aumentando man mano che l’incrudimento prosegue.
Nell’incrudimento cinematico l’ampiezza della zona elastica resta costante, ed un incrudimento al positivo implica una analoga riduzione (in valore assoluto) della tensione di snervamento al negativo.
L’incrudimento misto è una via di mezzo tra i due tipi di incrudimento.
E' possibile fare in modo che CURAN generi delle curve di tipo λ-spostamento oppure λ-azione interna, dove λ è un opportuno parametro di carico, ovvero è una frazione del carico totale. Per chiarire meglio, si veda l'esempio nella figura seguente, dove è mostrato il taglio T3 nel primo estremo dell'elemento beam numero 1, al crescere del carico.

Creazione delle curve
Per far creare a Curan le curve desiderate, è necessario selezionare preventivamente gli elementi opportuni (beam, truss, nodi) PRIMA dell'esecuzione dell'analisi nonlineare del modello in esame. Tali elementi devono essere selezionati nel serbatoio 3. (si veda l'argomento Come selezionare - Serbatoi di selezione).
Per ottenere la curva precedente, prima dell'analisi si dovrà dunque selezionare l'elemento beam numero 1 nel serbatoio di selezione 3. Assieme a essa verranno scritte le altre componenti elementari delle azioni interne, a entrambi gli estremi dell'elemento (N1, T21, T31, M11, M21, M31, N2, T22, T32, M12, M22, M32).
Se è selezionato anche un nodo prima dell'analisi, per quel nodo verranno scritte tre curve carico-spostamento lungo i tre assi di riferimento globali (TX, TY, TZ).
Vengono inoltre create le seguenti curve riferite alla intera struttura (elementi trave e biella):
1.Percentuale di volume plasticizzato della intera struttura in funzione del parametro di carico. Si ottiene sommando tutti i volumi plasticizzati degli elementi, moltiplicando per 100 e dividendo per il volume totale. E' un indice del danno subito dalla struttura.
2.Percentuale di volume rotto della intera struttura in funzione del parametro di carico.
Il volume plasticizzato di un elemento si ottiene con un integrale (di Lobatto) sull'asse dell'elemento, considerando le sole fibre plasticizzate e scartando le altre. In formula, se "i" è l'indice di integrazione di Lobatto, e "j" l'indice di fibra si ha:
![]()
dove Aj è l'area della fibra j-esima, Wi è il peso della integrazione di Lobatto, L è la lunghezza dell'elemento, e pij è un codice che vale 1 se la fibra è plasticizzata e vale 0 se non lo è. Tale codice muta al variare della fibra ed al variare della posizione della sezione lungo l'asse dell'elemento.
Analoga formula consente di ottenere il volume "rotto", dove però a pij va sostituito rij, che è 0 se la fibra non è rotta e 1 se lo è.
Oltre al volume totale plasticizzato e rotto, per ogni biella selezionata viene data la curva che dà la frazione di volume plasticizzato e rotto e la deformazione ε in funzione del parametro di carico. La deformazione ε può essere utilizzata (cfr. EC8, parte 3, B.5.2) come indice di danno per gli elementi biella dissipativi.
Per ogni elemento trave selezionato, oltre alle curve che danno le 12 componenti di sollecitazione (6 ad un estremo e 6 all'altro) in funzione del parametro di carico, vengono date le curve che danno la frazione di volume plasticizzato in funzione del parametro di carico, e la frazione di volume rotto in funzione del parametro di carico.

Inoltre viene data la rotazione cumulativa subita dall'elemento (elastica più plastica), in milliradianti, nei due piani principali, θ2c e θ3c. Queste rotazioni sono calcolate integrando la curvatura lungo l'asse dell'elemento con la formula (che usa la integrazione di Lobatto):
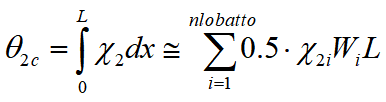
ed analogamente per θ3c usando χ3.La rotazione cumulativa tiene conto dello scorrimento plastico e quindi è correlata alla quantità di rotazione plastica delle cerniere plastiche. Si tratta di una misura della deformazione ed è un indice di danno sull'intero elemento. Ad esempio nella figura precedente si vede che la rotazione cumulativa giunge ad un picco di 18.7 mRad, e che l'andamento elastico viene abbandonato (in λ=1.4, θ2c=1.93mRad) a causa della plasticizzazione. Al termine della prima stazione (λ=1, carichi non sismici) l'elemento aveva subito una rotazione cumulativa di 0.8mRad. Da quel punto il ramo elastico viene presto abbandonato dando luogo a un vistoso scorrimento plastico, stimabile in circa 18.7-1.93≅16-17mRad.
Ulteriori informazioni sul tipo di danno subito dalle fibre si possono trarre rappresentando, con il comando Post-Fibre-Mostra Deformazioni Sezione, le deformazioni sulle varie sezioni dell'elemento dissipativo (vedi ad esempio in figura una parte della sezione è rotta).

I set di curve appena descritti si riferiscono a una singola stazione di carico (caso o combinazione). Se nel modello ci sono n stazioni, tutti i set di curve saranno ripetuti n volte (ad esempio, le tre componenti di spostamento del nodo i saranno ripetute per le n stazioni).
Selezionando preventivamente nel serbatoio 3 tutti i nodi e gli elementi (beam, truss) opportuni, durante l'analisi CURAN stamperà tutte le relative curve in uno o più file con estensione .PMC, in base al numero di stazioni di carico presenti. Se c'è una sola stazione, avrò un solo file .PMC, se le stazioni sono 10, i file .PMC saranno altrettanti.
Dato un modello Sargon chiamato [nome_modello].wsr, i file delle curve si troveranno nella stessa cartella e saranno così nominati:
[nome_modello].STATION_0001.PMC
[nome_modello].STATION_0002.PMC
[nome_modello].STATION_0003.PMC
ecc.
dove il numero progressivo corrisponde al numero di ciascuna stazione. Ogni file è quindi una collezione di curve che si riferiscono a una stessa stazione. Tutte le collezioni conterranno lo stesso numero e lo stesso tipo di curve. Le medesime curve differiranno nelle diverse collezioni per via dei diversi carichi applicati.
Visualizzazione delle Curve
Abbiamo visto come chiedere a Curan le curve che ci interessano e come il solutore le scrive in opportuni file. Veniamo ora alla visualizzazione delle curve contenute nei file .PMC:
Le curve in funzione del parametro di carico λ, scritte su richiesta da Curan durante l'analisi, sono visualizzabili direttamente in Sargon, attraverso il comando Curve del menu Post. Alla sua esecuzione viene proposto un opportuno dialogo, in cui si seleziona il file .PMC desiderato e si possono visualizzare le curve in esso contenute, a una a una. Si possono anche ottenere informazione sulle curve stesse e le si possono stampare su file di testo. Per la descrizione operativa del dialogo si rimanda all'argomento dedicato.

Note
•I punti che descrivono l'andamento delle curve non sono necessariamente equispaziati, ma dipendono dalle impostazioni sul passo di carico e dalle modalità di raggiungimento della convergenza durante il calcolo.
•Se si attiva il load path, le curve non vengono create.
Dopo aver eseguito con Curan un'analisi nonlineare che include la modellazione a fibre di elementi beam, è possibile visualizzarne i risultati in termini di tensioni, elemento per elemento e sezione per sezione, attraverso il comando Post-Fibre-Mostra sforzi sezione ![]() . Esiste un analogo comando per vedere le deformazioni (Post-Fibre-Mostra deformazioni-sezione). Per poter eseguire il comando è necessario che uno e un solo elemento beam sia selezionato.
. Esiste un analogo comando per vedere le deformazioni (Post-Fibre-Mostra deformazioni-sezione). Per poter eseguire il comando è necessario che uno e un solo elemento beam sia selezionato.
La forma sezionale dell'elemento correntemente selezionato viene visualizzata nella vista di Sargon. La sezione è modellata come un insieme di fibre, la cui forma dipende dal tipo di sezione in esame:
•fibre rettangolari, usate per modellare la maggior parte delle sezioni (piatti, angolari, sezioni a T o ad H, sezioni rettangolari cave, ecc.);
•fibre circolari in corrispondenza dei raccordi curvilinei (ad esempio quelli di una sezione ad H laminata);
•fibre con forma di settore di corona circolare, per modellare sezioni circolari piene o cave. La sezione è suddivisa in un certo numero di corone circolari concentriche, e ciascuna corona è suddivisa in un certo numero di settori. Ogni corona circolare è divisa in un numero generalmente diverso di settori, in base al suo diametro medio; per questo motivo, le fibre delle varie corone non sono necessariamente allineate sugli stessi raggi. Ciò è necessario per avere fibre di dimensione omogenea in tutte le zone della sezione.
Le immagini seguenti mostrano i vari tipi di fibre; per maggiore chiarezza, gli sforzi nelle sezioni sono nulli.

Sezione ad H saldata modellata con fibre rettangolari

Raccordi curvilinei di una sezione ad H laminata modellati con fibre circolari

Sezione circolare cava modellata con fibre aventi forma di settori di corona circolare
Nella parte in alto a sinistra della vista sono riportate le seguenti informazioni:
•numero dell'elemento beam;
•numero della sezione (corrispondente al numero del punto di Lobatto);
•ascissa adimensionale (csi) della posizione del punto di Lobatto lungo l'asse dell'elemento (+1.0 e -1.0 sono le ascisse adimensionali dei due estremi dell'elemento, 0.0 è il punto in mezzeria; se i punti sono più di 3, si avranno le ascisse corrispondenti agli ulteriori punti);
•numero del caso di carico;
•tensione normale massima;
•tensione normale minima.
La tensione normale massima e la tensione normale minima sono riportate anche sulla sezione, in corrispondenza dei punti dove si manifestano.
Ogni fibra della sezione è campita con un colore dipendente dal livello di tensione. In questo modo è possibile cogliere l'andamento delle tensioni nella sezione, nonché la posizione dell'asse neutro in caso di flessione (retta o deviata). Se una fibra ha tensione normale nulla, essa risulterà bianca.

Sforzi nelle fibre

Sforzi nelle fibre (dettaglio)
Per ogni elemento beam sono disponibili n sezioni, dove n è il numero di punti di Lobatto richiesti nelle impostazioni dell'analisi nonlineare. Per passare da una sezione all'altra si usano i comandi Sezione successiva e Sezione precedente, eseguibili anche con i bottoni ![]() .
.
- Per il momento il solutore gestisce le seguenti tipologie di sezione nel caso in cui siano necessarie le fibre:
o sezioni a I o H laminato;
osezioni a I o H saldato;
osezioni rettangolari;
osezioni circolari cave;
osezioni a cassone;
osezioni RHS;
osezioni a C saldato;
osezioni a C laminato e ali parallele (no rastremazione)
osezioni a T saldato;
osezioni a T ottenute per taglio di sezioni a I o H laminato;
osezioni a I o H laminato e ali di larghezza diversa (ASB);
in seguito saranno probabilmente aggiunte più sezioni (ad esempio le formate a freddo con opportune trattazioni, le sezioni in c.a. o fibro-rinforzate e le composte) e funzionalità.
Nota
Come descritto in precedenza, le sezioni circolari sono modellate con fibre che sono settori di corone circolari, e ciascuna corona è divisa in un numero generalmente diverso di fibre, in base al suo raggio medio. Ciò significa che non sono necessariamente presenti delle simmetrie radiali per le fibre. Nel caso riportato nell'immagine seguente, ad esempio, una sezione circolare cava è sottoposta a flessione. Nella zona a cavallo dell'asse neutro, la discretizzazione delle fibre è diversa tra la parte destra e quella sinistra della corona circolare. In particolare, a sinistra si hanno 3 fibre esattamente in corrispondenza dell'asse neutro, aventi quindi tensione nulla. Questo non avviene dall'altra parte, dove le fibre sono al di sopra o al di sotto dell'asse neutro, e quindi non possono avere tensione nulla.

Sforzi nelle fibre (dettaglio)
10 CRITERI DI USO DI CURAN
CURAN è dato in due versioni. La versione LIGHT e la versione FULL.
La versione LIGHT è data insieme al solutore statico lineare CLEVER e usa come elementi dotati di non linearità unicamente gli elementi biella e molla. I nodi semirigidi sono considerati elastici. Gli elementi trave, membrana, piastra sottile e spessa e solidi sono tutti elastici ed identici a quelli del solutore elastico lineare CLEVER.
La versione FULL viene sempre utilizzata se la chiave la abilita. Il file corrispondente all'eseguibile è lo stesso della versione LIGHT. La versione FULL utilizza i seguenti elementi:
-biella non lineare
- molla non lineare
-nodi semirigidi lineari o non lineari
-elemento beam elastico se il materiale è elastico lineare, altrimenti elemento beam a fibre, eventualmente con nodi semirigidi non lineari.
- elemento membrana elasto-plastico.
-elemento piastra (sottile o spessa) con integrazione di Lobatto nello spessore.
- elementi solidi
Nella analisi di elementi beam converrà partire da materiali elastici lineari. Se si ravvisa che i limiti elastici vengono superati, usando CURAN FULL, si può usare il modello a fibre. In tal caso se il tipo di sezione è gestibile a fibre, allora si può assegnare agli elementi beam un materiale non lineare e CURAN FULL userà la formulazione a FIBRE. Se viene assegnato un materiale non lineare, viene usato il modello a fibre anche se la non linearità non è attivata nel modello.
Dato che il modello a fibre è intrinsecamente meno preciso del modello elastico (poiché gli integrali di sezione sono calcolati come somma dei contributi delle singole fibre), ha senso usarlo solo quando è necessario, vale a dire solo se si supera la tensione di snervamento e si plasticizza almeno in parte la sezione.
11 RIFERIMENTI
[1] M.A. Crisfield, Non-linear Finite Element Analysis of Solids and Structures, Volume 1, Wiley, 2003
[2] M.A. Crisfield, Non-linear Finite Element Analysis of Solids and Structures, Volume 2 - Advanced Topics, Wiley, 1997
[3] Daniele Ferretti, Ivo Mori, Marco Morini, La stabilità delle strutture, McGraw-Hill, 2002