EC3: GUIDA TECNICA
VERSIONE EN:1993-1-1 (RILASCIATA CON LA VERSIONE 8.40 NEL NOVEMBRE 2007)
VERSIONE ENV (NON PIÙ RILASCIATA A PARTIRE DAL NOVEMBRE 2007).
_____________________________________________
VERSIONE EN:1993-1-1 (RILASCIATA CON LA VERSIONE 8.40 NEL NOVEMBRE 2007)
Sommario:
1 Generalità
2 Paragrafi implementati
3 Classificazione delle sezioni
4 Verifiche standard
4.1 Verifiche di resistenza
4.2 Verifiche di stabilità
4.2.1 Il problema dello svergolamento
4.2.2 Il nuovo formato delle verifiche di pressoflessione (metodo 1 e metodo 2)
4.2.3 Le verifiche di instabilità torsionale e flesso-torsionale (versione 9.90, Luglio 2012)
5 Verifiche utente
5.1 Approccio
5.2 Il file “ec3data.txt”
5.3 Esempio di aggiunta di una sezione al file: IPE500
6 Il tracciamento dei calcoli
7 L’uso di checksolvers
8 Le schede di validazione
9 Bibliografia
1 Generalità
L’aggiornamento del verificatore dalla versione ENV della norma alla versione EN ha richiesto un considerevole lavoro. La stesura di un verificatore in accordo ad EN1993-1-1 si presenta come un lavoro molto vasto e complesso, tenuto conto dei notevoli problemi di interpretazione e di applicazione che la norma pone, quando applicata in un contesto generale. Il problema è così vasto che sarà oggetto di una trilogia di pubblicazioni [1]-[3] delle quali al momento (novembre 2007) è disponibile solo la prima. Non si ritiene di poter dare in questa sede che indicazioni di massima, riservando alle pubblicazioni [1]-[3] l’approfondimento necessario.
Nel passaggio dalla versione ENV alla versione EN sono profondamente cambiate le formule di verifica a pressoflessione, e ciò ha posto considerevoli problemi di interpretazione e di applicazione. Inoltre, per le sezioni in classe 3, di fatto è stato ripristinato il calcolo tensionale puntuale tradizionale, sia pur con una mitigazione legata alla possibilità di redistribuire plasticamente le sollecitazioni taglianti e torcenti applicate.
I maggiori problemi riguardano la mancata generalità di numerose parti che sono state messe a punto avendo in mente problemi particolari. Le stesse formule di pressoflesisone non sono di fatto applicabili se non a profili doppiamente simmetrici. Si tratta di una grave limitazione, che non è mitigata da alcuna formula alternativa.
Il lavoro di studio e approfondimento ha abbracciato alcuni mesi. Da questo lavoro è scaturita anche una serie di importanti migliorie rispetto alla versione ENV precedentemente rilasciata. Tali migliorie sono le seguenti:
• È stata inclusa la torsione che precedentemente non era nominata dalla norma;
• Sono stati affrontati tutti i complessi problemi di interazione tra taglio e torsione anche se non chiariti dalla norma;
• È stato aggiunto il tracciamento dei calcoli, una funzionalità che consente di ricostruire passo passo i calcoli fatti e di disporre della gran parte dei risultati intermedi;
• Sono state messe a punto ben 100 schede di validazione ed alcuni worked example, che entreranno a far parte della documentazione del programma non appena pubblicate ufficialmente in [2] e [3], oggi in corso di stesura;
• E’ stato ampliato enormemente il raggio di azione del programma consentendo la esecuzione di verifiche utente su sezioni di forma qualsiasi;
• E’ stata migliorata la parte relativa al calcolo a svergolamento;
• E’ stata data la possibilità di usare vari tipi diversi di calcoli, scegliendo il miglior modo di eseguire il verificatore.
• E’ stata aggiunta a checksolvers la possibilità di eseguire controlli sui coefficienti di sfruttamento ottenuti con la norme EC3.
2 Paragrafi implementati
3.2.3 (per spessori t>80mm si è assunta una riduzione di 40N/mmq); 3.2.6, 5.5.2, 6.2.1 (ma non (2) e (10)), 6.2.2.1, 6.2.2.2 (l’area netta è tenuta in conto da un fattore riduttivo dell’area lorda), 6.2.2.5 (1) (2) i formati a freddo sono fuori dal campo di applicazione, (3), (4); 6.2.3; 6.2.4; 6.2.5; 6.2.6 ad esclusione delle clausole (5) applicata sempre e (6); 6.2.7 ma tenendo solo conto della torsione primaria; 6.2.8; 6.2.9.1 (ma non clausola (4)); 6.2.9.2; 6.2.9.3; 6.2.10; 6.3.1.1; 6.3.1.2 ma non clausola (4);6.3.1.3; 6.3.1.4; 6.3.2.1; 6.3.2.2.;6.3.2.4. per alcuni profili prendendo kc=1 clausola (2) e (3); 6.3.3.; annesso A; annesso B
3 Classificazione delle sezioni
A parte qualche piccola differenza nella definizione dei rapporti larghezza spessore, e, conseguentemente, nella definizione dei limiti, il problema della classificazione è stato affrontato in modo identico a quanto già previsto dalla precedente versione del verificatore. L’argomento è molto complesso quando affrontato nella sua generalità, ed è stato oggetto di una specifica pubblicazione ([1]) che costituisce il fondamentale riferimento bibliografico dal quale trarre tutte le informazioni del caso.
Nella documentazione del programma è disponibile l’articolo [articolo1], che originariamente fu scritto per spiegare la metodologia impiegata.
SARGON risolve completamente il problema nel caso di sezioni ad I ed H laminato ed a I saldato (IPE, HEA, ecc.) così come chiarito in [1], mentre relativamente agli altri profili SARGON assume come classe la massima classe tra quelle dovute a sollecitazioni pure (sola N, solo M2, solo M3). Nel caso di elementi biella SARGON assume come classe la classe 1 se l'elemento è in trazione, la classe a compressione semplice in caso contrario.
Il caso di classe 4 è da considerare un caso a sè. Il calcolo delle grandezze efficaci viene eseguito per tutte le tipologie di profilo ad esclusione dei profili formati a freddo generici (per i quali esiste uno specifico servizio di calcolo a richiesta), dei profili ottenuti per composizione di sezioni, dei profili ottenuti per composizione di poligonali. Negli altri casi tali grandezze sono poste eguali a zero. E’ tuttavia sempre possibile mediante le verifiche utente definire i moduli di resistenza efficaci pertinenti.
I profili del tipo formato a freddo generica, composta generica e composta da poligonali, e non sia un profilo-utente (che può sempre essere verificato) viene considerato non verificato, ed a esso è associato il coefficiente di sfruttamento convenzionale 99.
Profili che non siano doppiamente simmetrici presentano particolari problemi allorchè ci si trovi a calcolarne le grandezze efficaci. In tal caso infatti, anche sotto sollecitazioni semplici, gli assi principali della sezione efficace sono ruotati rispetto a quelli della sezione lorda, facendo con ciò perdere un pò di vista il significato delle verifiche a stabilità.
Quando per profili classificati in accordo a quanto chiarito nell’articolo citato uno qualsiasi di questi tre rapporti, in valore assoluto
N/Npl M2/M2pl M3/M3pl
è minore di 1.e-4 (0.0001), allora la corrispondente componente di sollecitazione è assunta nulla ai fini della classificazione. Tale accorgimento evita che compressioni puramente numeriche (piccoli valori di compressione in presenza di momento nullo) possano portare a classificazioni troppo severe.
4 Verifiche standard
Con il nome di “verifiche standard” si intendono tutte quelle verifiche che vengono eseguite sui profili in modo automatico ovvero senza che l’utente “insegni” al programma come fare. Chiaramente, data l’estrema complessità della norma, è talvolta necessario impiegare “sezioni utente” al fondamentale fine di chiarire in che modo trattare profili di forma particolare, oppure al fine di specializzare le verifiche secondo i propri desideri. Sono verificate automaticamente le seguenti sezioni:
•A I o H laminato in tutte le classi.
•A I o H saldato in tutte le classi
•A T saldato in tutte le classi.
•A T laminato ottenuto per taglio di profili a I o H laminato, in tutte le classi.
•A I laminato con ali diseguali in tutte le classi.
•Piatti.
•Sezioni circolari cave in classe 1, 2 o 3.
•Sezioni rettangolari cave saldate o laminate (Rhs) in tutte le classi.
•A C laminato (ali rastremate o no) o saldato in tutte le classi
•A Z formato a freddo in classe 3 o 4.
•A L formato a freddo in classe 3 o 4.
•A C formato a freddo in classe 3 o 4.
•A L laminato, o saldato in tutte le classi.
•A doppio o quadruplo L e a doppio o C .
Non sono verificate automaticamente, a meno che non siano definite come sezioni utente, le seguenti sezioni:
•Composta generica
•Formata a freddo generica
•Composta da poligonali
•Totalmente generica
4.1 Verifiche di resistenza
4.1.1 Sezioni in classe 1 o in classe 2
Per queste sezioni vengono utilizzati, dove disponibili, domini nonlineari eventualmente corretti per tener conto della presenza di taglio e torsione. Nel caso in cui tali domini non siano disponibili viene impiegata una formula di interazione di tipo lineare, corretta per tener conto della presenza di taglio e momento torcente. In questo caso gli sfruttamenti plastici vengono calcolati impiegando una tensione di snervamento ridotta (1-ρ2-ρ3)fy al posto della tensione di snervamento originaria. Di solito gli sfruttamenti calcolati non sono coefficienti di sfruttamento ma meri indici di sfruttamento, essi non esprimono cioè una reale distanza dalla soglia. Per una estesa trattazione del problema, non sintetizzabile nelle note di rilascio di un programma, si rimanda a [3].
4.1.2 Sezioni in classe 3
In questo caso le verifiche sono verifiche puntuali ed il criterio adottato è quello di Von Mises. Le sezioni si dividono in due gruppi: il gruppo delle sezioni per le quali vengono adottate delle verifiche convenzionali, ottenute sovrapponendo le tensioni normali e tangenziali in modo che siano a favore di sicurezza; ed il gruppo di sezioni per le quali viene definito un insieme di punti nei quali vengono definiti dei moduli di resistenza generalizzati atti a far calcolare la tensione normale e la tensione tangenziale, combinate poi con la regola di Von Mises.
Al primo gruppo appartengono le sezioni: circolari; a [], a ][, angolari composti a T ed a croce, nonchè angolari semplici;
Al secondo gruppo appartengono le sezioni ad I o H laminato, ad I o H saldato, a T laminato o saldato, RHS (rectangular hollow section), a cassone, piatti o rettangolari, ed UPN nonché C saldati.
Poiché la norma consente una redistribuzione plastica anche nel caso di calcoli elastici in nessuno di questi casi la tensione tangenziale dovuta al taglio è calcolata usando la formula di Jouravskij. Invece viene sempre adottata una ripartizione costante.
4.1.3 Sezioni in classe 4
Alcune tipologie di sezione possono essere verificate anche se di classe 4. Tali tipologie sono:
•profili a I o H laminato;
•profili ad I o H saldato;
•profili ad I o H laminato a flange asimmetriche;
•profili ad U saldato, laminato e formato a freddo;
•profili a T ottenuti per taglio di profili ad I o H laminato;
•profili a T saldato;
•profili a cassone;
•profili rettangolari cavi (RHS);
•Profili a C a flange parallele.
•Profili formati a freddo a Z, L e C.
Perché questi profili siano verificati automaticamente benché in classe 4, il verificatore deve poter conoscere i valori efficaci. I valori efficaci vengono calcolati dal programma automaticamente. Tali valori efficaci dipendono anche dal materiale e quindi non possono essere considerati una proprietà della sezione immutabile, ma piuttosto sono una proprietà della sezione una volta che sia noto il materiale con cui è costituita.
Per far conoscere i valori efficaci di un profilo ricandente nelle tipologie anzi dette, l'utente deve eseguire il comando Edit-Proprietà-Modifica sezione scegliere la sezione a cui è interessato e poi premere il bottone "Valori Efficaci".
A quel punto si apre un opportuno dialogo che chiede essenzialmente le tensioni di snervamento e rottura del materiale e il valore di γm0 da usare. L'utente dovrà introdurre i valori che corrispondono agli elementi a cui quella sezione è stata assegnata. Se la sezione è stata assegnata a elementi aventi materiale diverso, sarà necessario (se per tutti è necessario un calcolo in classe 4) distinguere i profili introducendo nuovi profili identici a con nome diverso.
Ad esempio se gli elementi A hanno la sezione HE200B in S235 e gli elementi B hanno la stessa sezione in S355, agli elementi B si potrà assegnare una sezione "HE200B_2" in modo da poter definire due volte i valori efficaci, una volta (HE200B) con S235, ed una volta (HE200B_2) con S355.
Il verificatore utilizzerà comunque i valori efficaci pertinenti che calcola in modo automatico.
Nel caso in cui sia presente anche taglio e torsione la formula viene corretta riducendo da 1 a (1-ρ2-ρ3) la soglia massima. In questo caso
![]()

E di conseguenza ρ3.
4.2. Verifiche di stabilità
Le formule di stabilità presenti nell’Eurocodice 3 sono relative alle verifiche di compressione, di svergolamento, di pressoflessione con o senza svergolamento. Per quanto riguarda la verifica di compressione semplice questa non presenta particolari difficoltà nota che sia la snellezza e la curva di stabilità da adottare per la verifica. Ove l’azione assiale sia variabile il programma assume la massima compressione come valore di riferimento sulla membratura. Per quanto invece riguarda le verifiche di svergolamento e di pressoflessione, esistono considerevoli problemi che necessitano di essere menzionati.
4.2.1 Il problema dello svergolamento
Le verifiche a svergolamento possono essere eseguite essenzialmente mediante tre distinti metodi, in EN1993. Il primo metodo impiega una formula chiusa per il calcolo del momento critico; il secondo metodo impiega i moltiplicatori critici e limite ottenuti con calcoli di buckling e di analisi nonlineare; il terzo metodo, semplificato, verifica la piattabanda compressa. Il verificatore usa quando possibile il metodo che impiega la formula chiusa per il valore di Mcrit, mentre quando ciò non è possibile (sezioni utente o sezioni a C) si esegue di fatto una verifica della piattabanda compressa pensata isolata dal resto della sezione.
Il primo metodo può essere applicato solo a sezioni inflesse nel piano di simmetria, e consiste nell’applicare una complicata formula (non più esplicitamente presente nella norma) che può essere scritta come segue:

Se il carico è applicato nel centro di taglio zg=0. Inoltre per sezioni doppiamente simmetriche zj=0. In questi casi la formula precedente si semplifica e viene unicamente a dipendere dal coefficiente di distribuzione C1. Il termine kw è un coefficiente che vale 1 quando l’ingobbamento è libero agli estremi, 0,5 se è impedito. Il coefficiente β1 (anche indicato da k, in alcune fonti), dà conto della lunghezza compresa tra due ritegni torsionali successivi e di solito coincide con 1. Il termine Iw è la costante di ingobbamento mentre It è il momento di inerzia torsionale.
Nel caso di sezioni ad I o ad H laminato ed a I saldato, la formula precedente fornisce direttamente il valore del momento critico elastico associato allo svergolamento. Tale formula dipende, come si è detto, dal coefficiente di distribuzione C1 che per momento costante vale 1 mentre per momento variabile è generalmente maggiore di 1. Sebbene siano disponibili tabelle capaci di fornire questo coefficiente in una certa casistica, nella maggior parte dei casi tale coefficiente non risulta determinabile in modo semplice. Alcuni studi, eseguiti su un gran numero di simulazioni numeriche, hanno permesso di mettere a punto delle formule semplificate che, campionando il diagramma di momento M associato allo svergolamento (di solito M2) esprimono C1 in forma chiusa.
Tra queste formule l’ultima e più attendibile è quella di Serna (vedasi il dialogo che consente di scegliere il modo in cui valutare C1). Altre formulazioni sono dovute a Kirby-Nethercot (norme americane) ed alle normative BS.
Il programma verificatore è in grado di calcolare C1 partendo da una generica distribuzione di momento, mediante l’uso delle formule anzi dette. E’ anche possibile fissare un valore unico e costante per C1.
Calcolato il momento Mcrit (che come si vede dipende dalla combinazione a causa della dipendenza di C1 dal diagramma di momento sollecitante). Il programma può calcolare la snellezza per lo svergolamento λLT e da questa un coefficiente riduttivo da applicare al momento limite per ottenere la soglia di momento da associare alla instabilità laterale per svergolamento.
Quando viene applicato il metodo della piattabanda compressa, di fatto si valuta la snellezza di questa mediante il suo raggio di inerzia if. Anche in questo caso è previsto un coefficiente, denominato kc, che consente di dosare la verifica in funzione della distribuzione di momento, ma, data l’indisponibilità di formule generali per la sua valutazione esso, a favore di sicurezza, viene posto eguale ad 1.
4.2.2 Il nuovo formato delle verifiche di pressoflessione (metodo 1 e metodo 2)
Le nuove norme EN differiscono dalle precedenti ENV in specie per il formato delle verifiche a pressoflessione, che è stato profondamente cambiato pervenendo, nella intenzione degli autori, ad un formato al tempo stesso più chiaro e più accurato. In realtà da un punto di vista operativo il nuovo formato si presenta notevolmente complesso e macchinoso, tanto che di fatto risulta inapplicabile a mano. Inoltre il nuovo formato si riferisce a sezioni doppiamente simmetriche mentre non è ben chiaro come regolarsi quando il profilo da verificare possegga un solo asse di simmetria o al limite nessuno.
Il formato generale delle verifiche prevede due formule, una per lo sbandamento nel piano 1-2 ed una per lo sbandamento nel piano 1-3. Queste formule devono poi essere diversamente applicate a seconda che il profilo sia in classe 1 o 2 o in classe 3, ed a seconda che lo svergolamento sia considerato possibile o impedito. Inoltre le formule generali vengono poi a specializzarsi in due differenti approcci, che comportano due metodi differenti per il calcolo dei coefficienti: un formato denominato “Metodo 1”, e dovuto alla ricerca franco-belga, ed un formato denominato “Metodo 2” e dovuto alla ricerca austro-tedesca.
Il formato generale delle verifiche è il seguente:
I due metodi differiscono per il modo in cui vengono calcolati i coefficienti kij. Nelle formule precedenti le grandezze a denominatore cambiano in funzione della classe. Per la classe 1 e 2 si usano i moduli plastici, per la 3 quelli elastici e per la 4 l’area ed i moduli di resistenza efficaci. Le variazioni di momento Δ sono nulle se la classe non è la 4.
Il verificatore è in grado di applicare entrambi i metodi, a scelta (vedasi il dialogo opportuno).
Data la possibilità di eseguire i calcoli con entrambi i metodi, si consiglia di avvalersi di tale funzionalità come procedura standard onde migliorare il grado di affidabilità dei calcoli. Tra i due metodi quello maggiormente affidabile e preciso dovrebbe essere, nella maggior parte dei casi, il metodo franco-belga (il metodo 1).
Vediamo nel seguito in che modo i due metodi provvedano a calcolare i coefficienti.
4.2.2.1 Metodo 1 (franco-belga)
Le formule che danno i coefficienti kij sono molto complesse, in specie nel caso di dimensionamento plastico. Non è questa la sede per entrare nel dettaglio, ci si limita ad osservare che in questo approccio la dipendenza dei coefficienti da ciascun fenomeno fisico (plasticità, svergolamento, distribuzione di momento, ecc.) è chiaramente evidenziata da termini a questi associati. Particolare rilevanza hanno le formule che si riferiscono al calcolo dei coefficienti Cmi,0 per le quali (cfr. tabella A.2 della norma) esiste una dipendenza dalla freccia massima sotto i carichi applicati, almeno nel caso in cui la distribuzione di momento non sia lineare. La formula è questa:

nella quale compare il massimo momento e la massima freccia δ. La massima freccia δ può essere valutata in varii modi (vedasi il dialogo opportuno). Il programma ne propone due: una frazione costante della luce ed un valore ottenuto integrando l’equazione della linea elastica.
Si segnala che la formula per il coefficiente Czz presente nel testo della norma oggi (novembre 2007) disponibile, contiene un errore. Tale errore è stato corretto e non figura nel verificatore.
4.2.2.2 Metodo 2 (austro-tedesco)
Nelle intenzioni degli Autori, il metodo austro tedesco dovrebbe consentire una maggior semplicità d’uso rispetto a quello franco-belga. In effetti la sua applicazione nei calcoli a mano è più semplice, benchè, a nostro parere, pur sempre proibitiva. Relativamente a questo metodo si deve segnalare una certa equivocità nella definizione dei coefficienti αs ed αh, dovuta ad una non piena comprensibilità della tabella B.3. Anche nella tabella B.3 figura un errore corretto nel verificatore (nell’ultima riga ed ultima colonna il termine 0,9-…. Deve essere sostituito da 0,9+…). Un motivo di serio imbarazzo nell’applicazione del metodo è la ambiguità nella definizione dei coefficienti Cm legata alle differenti formule previste per il caso di “carico uniforme” e “carico concentrato”. In realtà, come è ben evidente, il caso normale è quello in cui sono presenti entrambi. Il programma assume sempre che il caso sia quello di carico uniforme essendo questo più severo dell’altro.
4.2.3 Le verifiche di instabilità torsionale e flesso-torsionale (dalla versione 9.90, Luglio 2012)
Un elemento soggetto a compressione semplice può instabilizzarsi mediante due modalità dette torsionale e flesso-torsionale. Tali modalità sono diverse dalle modalità flessionali tipiche del problema di Eulero. Queste modalità di instabilizzazione sono assenti normalmente nella maggior parte dei profili di impiego comune, tuttavia, per profili in parete sottile, esse possono rivelarsi determinanti ai fini delle verifiche. La situazione di compressione semplice deve dunque essere indagata sia per il rischio di instabilità flessionale, sia per il rischio di instabilità torsionale e flesso-torsionale.
La formula per il carico critico torsionale Ncr,T è la seguente:
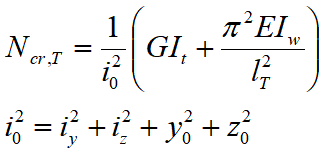
nella quale
G è il modulo di elasticità tangenziale.
It è il momento di inerzia torsionale primario.
E è il modulo di Young
Iw è la costante di ingobbamento
lT è identica alla lunghezza di libera inflessione per svergolamento, dominata dal coefficiente di libera inflessione β1
iy ed iz sono i raggi di inerzia si riferiscono agli assi principali 2 e 3 rispettivamente (iy=i2, iz=i3).
y0 è la coordinata del centro di taglio rispetto al baricentro lungo l'asse principale y (asse 2).
z0 è la coordinata del centro di taglio rispetto al baricentro lungo l'asse principale z (asse 3).
Nel caso in cui sia presente almeno un asse di simmetria, allora il carico critico Ncr,TF è esprimibile in forma chiusa, se non c'è nessun asse di simmetria allora la formula non è disponibile in forma chiusa. Se la simmetria è doppia allora Ncr,TF = Ncr,T. In caso contrario, nella ipotesi in cui l'asse di simmetria sia l'asse y (o asse principale 2), la formula per Ncr,TF è la seguente:
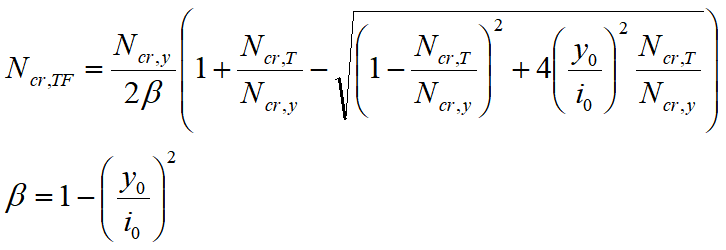
nella quale Ncr,y è il carico critico per instabilità flessionale attorno all'asse y (asse 2, di simmetria). Si noti che se y (2) è di simmetria allora z0=0.
Se invece la simmetria è relativa all'asse z (o asse 3, symmetry = 3), le formule diventano le seguenti:

Calcolati Ncr,y, Ncr,z con le ben note formule seguenti, relative al carico critico euleriano:

si ha infine il carico critico elastico
Ncr=min{Ncr,y, Ncr,z, Ncr,T, Ncr,TF}
Ad ognuno dei carichi critici è associata una curva di stabiltà. Per Ncr,T ed Ncr,TF si usa la curva associata all'asse 3.
Ne consegue che il carico di progetto finale Nb,Rd sarà dato, per le sezioni in classe 1, 2 e 3, da
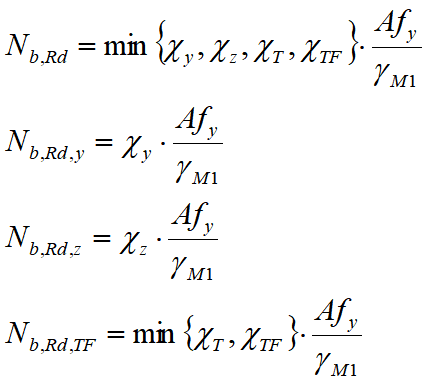
e per le sezioni in classe 4 da
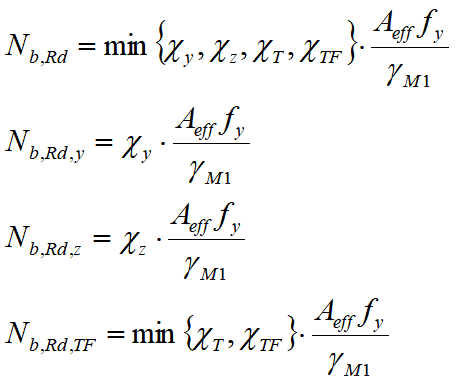
I coefficienti riduttivi χ si trovano nota la curva di stabilità e nota la snellezza adimensionale. Questa ultima è data, per le sezioni in classe 1, 2 e 3 da
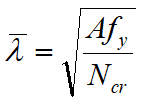
mentre per le sezioni in classe 4, da
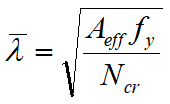
dove al posto di Ncr andrà messo il carico critico opportuno tra i 4 disponibili.
La verifica alla instabilità torsionale e flesso-torsionale viene fatta per alcune forme sezionali in modo automatico, mentre per altre no.
Per queste ultime, generalmente o sezioni non standard o sezioni non simmetriche. è sempre possibile utilizzare le sezioni utente e "spiegare" al programma come fare.
Per le seguenti sezioni il calcolo è fatto automaticamente (anche facendo uso di formule interne hard coded sia per il calcolo della posizione del centro di taglio, sia per il calcolo di Iw):
•sezioni a I o H laminate (doppia simemtria)
•piatti e sezioni rettangolari (doppia simmetria)
•tubi circolari (doppia simmetria)
•RHS (doppia simmetria)
•sezioni saldate a I o a H (simmetria asse 3)
•sezioni a T a lati rastremati (simmetria asse 3)
•sezioni a T saldate (simmetria asse 3)
•sezioni a T ottenute per taglio da sezioni ad I o ad H (simmetria asse 3)
•sezioni a U laminate (simmetria asse 2)
•sezioni a U saldate (simmetria asse 2)
•sezioni composte da 4 angolari a croce (doppia simmetria)
•sezioni composte da due angolari a _||_ (simmetria asse 3)
•sezioni a L laminato a lati eguali (simmetria asse 2)
•sezioni a L saldato a lati e spessore eguale (simmetria asse 2)
•sezioni formate a freddo a C, L e Z.
Una volta calcolato Nb,Rd occorre ben comprendere come questo viene utilizzato.
Per elementi biella esso è il carico assiale effettivamente sopportabile (non c'è interazione con il momento flettente).
Per elementi trave il dato è utilizzato per una verifica iniziale sull'effetto della azione assiale presa da sola, e viene poi impiegato o meno a seconda di quale formula si usi per la presso-flessione:
•se si usano i Metodi 1 e 2 di Eurocodice 3, nelle formule di interazione si prendono in considerazione solo Nb,Rd,y e Nb,Rd,z.
•se si usano le NTC Metodo A, allora nelle formule di interazione si prendono in considerazione solo Nb,Rd,y e Nb,Rd,z.
•se si usano le formule della versione ENV, allora il primo termine ha a denominatore Nb,Rd e dunque si tiene anche conto di Ncr,T e Ncr,TF..
Limitatamente ai soli elementi formati a freddo la EN 1993-1-3 dà una formula di interazione per la presso flessione, che tiene anche conto delle modalità di instabilizzazione torsionale e flesso-torsionale. La formula è la seguente:
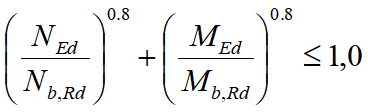
tale formula non è al momento ancora implementata dal verificatore, dato che è una formula di presso-flessione retta e non deviata come necessario.
| 5.1. | Approccio |
La complessità delle formulazioni previste nella norma e la loro mancanza di esaustività da un lato, l’esigenza di personalizzare e specificare meglio le verifiche dall’altro, ha portato alla necessità di mettere a punto un formato di verifica più generale, che consentisse in tutti i casi di poter eseguire verifiche automatiche usando un formato praticamente coincidente con quello della norma. Si è quindi dovuto mettere a punto un insieme di regole e di parametri di nuova concezione, in grado di consentire all’utente di lavorare con qualsiasi forma sezionale. Tale ampliamento è stato molto complicato ma realizza un importantissimo obiettivo, in specie quando usato in congiunzione con la funzionalità del tracciamento. Il verificatore automatico diviene uno strumento di lavoro personalizzabile ed adattabile alle più svariate esigenze.
Da un punto di vista pratico il funzionamento è il seguente (affine a quanto avviene per le CNR e per le BS). Se una sezione figura all’interno di un file denominato “EC3DATA.txt” e collocato nella cartella di installazione del programma, questa sezione non viene verificata impiegando le regole normali ma applicando delle regole di verifica particolari. Tutti gli elementi e le membrature che utilizzano quella sezione saranno verificate impiegando queste regole particolari e non le regole normali previste dal verificatore. Ciò vale per tutti i profili, anche quelli standard: è sufficiente che il nome del profilo figuri all’interno del file EC3DATA.TXT in un opportuno blocco di istruzioni, perché questo venga trattato in modo diverso e verificato con le regole utente.
Naturalmente è sempre possibile attivare o meno questa opzione semplicemente cambiando il nome delle forme sezionali all’interno di EC3DATA.TXT in modo che siano/non siano identiche a quelle definite nel modello del programma. In linea di principio sarebbe possibile bypassare completamente il normale funzionamento del verificatore, semplicemente includendo le forme sezionali nel file EC3DATA.TXT. Produttori che abbiano particolari profili o particolari esigenze di verifica possono creare o commissionare programmi in grado di compilare da soli il file EC3DATA in modo da personalizzare pienamente le verifiche.
Una analitica rassegna del formato del file potrà consentire di comprendere in che modo debba essere compilato il file, il successivo paragrafo dà invece un esempio di compilazione relativo ad un profilo IPE500. Dalla versione 9.60 non é più necessario gestire manualmente il file EC3DATA.txt: é infatti disponibile un comando che attraverso un'opportuna interfaccia guida l'utente nella compilazione del file in modo più semplice e veloce.
In quanto segue verranno fornite le spiegazioni necessarie a comprendere il significato dei dati da introdurre nel file. A tale fine verranno essenzialmente trattati i seguenti problemi, dal punto di vista di chi deve verificare un profilo generico:
| • | Il problema della classificazione; |
| • | Il problema delle verifiche di resistenza; |
| • | Il problema delle verifiche a stabilità con particolare riguardo per lo svergolamento |
Il problema della classificazione
In generale la classificazione di un piatto sotto l’azione di una certa distribuzione di tensione, plastica o elastica, può essere espressa da disequazioni del tipo
(c/t)< f(ε)
dove c/t è il rapporto larghezza spessore per il piatto considerato ed f() è una opportuna funzione delle caratteristiche geometriche del profilo impiegato nonché della classe considerata. La precedente relazione può essere invertita fornendo una disequazione di questo tipo:
ε > g(c/t)
essendo g una opportuna funzione del rapporto larghezza spessore e dei dati geometrici della sezione. Ad ogni sollecitazione elementare può essere associato un valore e di soglia oltre il quale la sezione deve essere classificata, per quella data sollecitazione, con una classe superiore. Si consideri ad esempio un profilo a T che in flessione plastica comporti, per flessione positiva, un tratto compresso pari a 0,6 volte l’altezza dell’anima ed un tratto teso pari a 0,4 volte tale altezza. In questo caso potremo scrivere per la delimitazione tra classe 2 e 3:
c/t < 456ε/(13x0,6-1)
Tale equazione può essere invertita fornenedo:
ε> (c/t)(13x0,6-1)/456=0,0149(c/t)
ed ammettendo che c/t sia pari a 50
ε> 0,7456
Questa disequazione vuol dire che l’anima potrà essere classificata in classe 2 per flessioni positive, solo a patto che il materiale impiegato soddisfi la condizione, precedente che si traduce nella seguente:

e quindi di fatto
![]()
Nel caso in cui la flessione inverta il suo segno, le precedenti considerazioni devono essere modificate come segue:
c/t < 456ε/(13x0,4-1)
ε> (c/t)(13x0,4-1)/456=0,00921(c/t)=0,46052
dal che si evince che il valore di soglia per e cambia a seconda del segno del momento flettente applicato.
Il ragionamento fatto per un piatto può essere ripetuto per tutti i piatti componenti la sezione, pervenendo infine ad una condizione che inviluppi tutte le altre sempre del tipo
ε>epsM2p
Pensando al momento positivo secondo l’asse 2. Analoga quantità limite per la classe 2-3 potrà essere definita per tutte le componenti di sollecitazione, in particolare per l’azione assiale (epsN) per il memento M2 positivo (epsM2p) e negativo (epsM2m) e per il momento M3 positivo (epsM3p) e negativo (epsM3m). Tali quantità limite, tutte associate al passaggio tra la classe 2 e la classe 3 mettono in condizione il verificatore di classificare il profilo noto che sia il materiale ad esso applicato. Basterà calcolare il valore di ε del materiale in questione e poi confrontare tale numero con le soglie specificate.
Il problema della classificazione sotto sollecitazioni elementari viene così ad essere affrontato in modo sistematico e formale mediante la definizione del limite di snervamento dell’acciaio da usare per ottenere una certa classe.
Come è noto (se si è letto il lavoro [1]) il problema della classificazione sotto sollecitazioni miste è tutt’altro che banale ed è stato affrontato al momento solo per le sezioni ad I laminato e saldato (I ed H). Per le sezioni generiche l’algoritmo che classifica il profilo quando assoggettato ad una terna di sollecitazioni del tipo (N, M2, M3) è diverso. Per ogni sollecitazione si valuta dapprima se questa è significativa. Per essere significativa deve superare un valore di soglia che è 1/10000 dei valori limite (Afy o Wfy). Se la sollecitazione è significativa se ne valuta il segno e si attribuisce la classe che le compete sulla base dei valori di ε di soglia specitficati. Infine si classifica il profilo con la massima classe tra quelle delle sollecitazioni elementari così valutate.
Il problema delle verifiche di resistenza
Il problema delle verifiche di resistenza per le sezioni utente consiste nell’”insegnare” al programma in che modo eseguire tali verifiche in tutti e tre i possibili casi che si possono presentare: sezione in classe 1 o 2; sezione in classe 3; sezione in classe 4.
Classe 1 o 2
Nel primo caso si può scegliere se adottare un dominio limite plastico linearizzato oppure no. Se il dominio plastico è di tipo non lineare, esso ricade nel formato specificato dalla norma, e richiede 20 distinti parametri per poter essere identificato. In genere molti di questi parametri sono nulli, ma taluni di essi possono assumere speciali valori da calcolarsi a mano. I parametri sono individuati da lettere comprese tra “A” e “V” secondo il formato seguente:

n= N / Npl,Rd
MN,2,Rd=Mpl,2,Rd x [ A + Bn + Cn2]
MN,3,Rd=Mpl,3,Rd x [ D + En + Fn2]

Una opportuna scelta dei parametri consente di sposare tutte le formule presenti nella normativa ed una ampia classe di domini plastici limite.
Nel caso in cui il dominio limite sia lineare la formula di verifica è la seguente:
![]()
Se non ci fossero la torsione ed il taglio il problema potrebbe dirsi risolto. In realtà tali domini sono entrambi bisognosi di modifiche per tenere in conto la possibilità che siano applicati tagli o momenti torcenti rilevanti.
Per fare questo si deve applicare la clausola della norma che indica di usare, per le aree resistenti a taglio, una tensione ridotta al valore (1-ρ)fy, dove ρ è un numero adimensionale funzione del livello di taglio e torsione applicati.
Purtroppo le prescrizioni di normativa sono deficitarie a riguardo della modifica da applicare alle formule che danno i domini in pressoflessione deviata, nella condizione di taglio rilevante. Si è quindi dovuta sviluppare una teoria ad hoc che abbracci il problema in modo generale. L’argomento è piuttosto vasto e non può essere trattato in questa sede se non per sommi capi.
Si definiscono dapprima i tagli plastici ridotti per tener conto della presenza della torsione:


Noti questi si possono definire i fattori ρ:


Se risulta ρi<0,5 si deve porre ρi=0.
Una volta calcolati questi parametri ρ è possibile modificare le formule che danno i domini limite in questo modo:
![]()
E per il dominio non lineare:

![]()
![]()
![]()
Dove i termini avi e wiplavj esprimono il rapporto tra le proprietà delle zone di sezione coincidenti con le aree resistenti a taglio ed i corrispondenti moduli resistenti sezionali. Pertanto:
![]()
![]()
![]()
![]()
![]()
![]()
Se non si vuole calcolare i wjplavi, è sempre possibile adottare per essi, a favore di sicurezza, il valore 1. Se si fa così anche per gli avi si perviene alle seguenti formule semplificate che tengono in conto anche taglio e torsione:
![]()
E nel caso di dominio non lineare:

![]()
![]()
![]()
Classe 3
In questo caso occorre definire i moduli di resistenza generalizzati per un certo numero di punti sulla sezione. Da questi moduli di resistenza generalizzati sarà poi possibile calcolare le tensioni normali e le tensioni tangenziali associate al taglio ed alla torsione. Infine verrà applicata la verifica di resistenza secondo Von Mises.
Precisamente si pone in ogni punto “i”:
x2i W3i=I3/x2i
x3i W2i=I2/x3i
At22 modulo di resistenza per calcolare la τ2 dovuta a T2.
At32 modulo di resistenza per calcolare la τ2 dovuta a T3.
W12 modulo di resistenza per calcolare la τ2 dovuta a M1.
At23 modulo di resistenza per calcolare la τ3 dovuta a T2.
At33 modulo di resistenza per calcolare la τ3 dovuta a T3.
W13 modulo di resistenza per calcolare la τ3 dovuta a M1.
E poniamo, in ogni punto di verifica “i”:
![]()
![]()
![]()
![]()
![]()
Se uno dei moduli A22, A32, W12, A23, A33,W13 viene convenzionalmente posto eguale a zero la corrispondente tensione viene posta eguale a 0 (e non a infinito).
Classe 4
In questo caso occorre dapprima insegnare al programma quali siano i valori efficaci dell’area e dei moduli resistenti a flessione. Questi ultimi possono in generale assumere valori diversi a seconda che la flessione sia positiva o negativa. Inoltre occorre specificare le distanze con segno del baricentro della sezione efficace rispetto a quella lorda, in modo che i momento aggiuntivi siano rispettivamente:
ΔM2=NxDe2
ΔM3=NxDe3
E’ da notare che i valori efficaci sono funzione della tensione di progetto. Essi dovranno quindi essere associati ad una certa tensione di progetto che dovrà corrispondere a quella dei profili effettivamente adottati nel modello da verificare.
In assenza di taglio e torsione le verifiche si scrivono in questo modo:
![]()
Il verificatore impiegherà il Weff pertinente anche in funzione del segno del momento applicato complessivamente. Si noti che tutti gli addendi devono essere positivi, e quindi la norma sottointende un valore assoluto in essa mancante.
In presenza di taglio e torsione, la verifica viene eseguita in modo semplificato con la seguente formula:
![]()
Dove ρ2 ed ρ3 sono stati definiti precedentemente quando si è parlato delle verifiche di resistenza in classe 1 o 2.
Il file EC3DATA.TXT è costituito da un insieme di blocchi che delimitano ogni forma sezionale. Ogni blocco comincia con la scheda _EC3SHAPE e termina con la scheda _ENDSHAPE. Sono possibili commenti, individuati da righe inizianti con “$” oppure posti in coda a una riga di dati a cominciare da un “;”.
Prima della versione 9.60 di Sargon era necessario compilare manualmente il file. Dalla 9.60 in poi é sempre possibile gestirlo manualmente, ma la modalità più immediata e comoda é l'utilizzo del comando Verifiche utente che attraverso opportuni dialoghi aiuta l'utente nell'inserimento dei dati nel file. Si rimanda alla spiegazione del comando per la descrizione dei dialoghi e delle operazioni necessari a una corretta compilazione, mentre questa sezione della guida é destinata alla comprensione dei parametri presenti nel file.
Qui di seguito si dà un esempio di file EC3DATA.TXT, che sarà anche utile per commentare le varie schede.
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
$ $
$ $
$ $
$ Eurocode 3 $
$ $
$ EN 1993-1-1:2005 $
$ $
$ $
$ USER'S SECTION DATA $
$ $
$ $
$ $
$ $
$ This file stores section data to be used for Eurocode 3 checks. Data $
$ teach solver how to perform checks within a general model which has $
$ been set up by Castalia srl. $
$ $
$ $
$ Card definitions: $
$ $
$ _EC3SHAPE name $
$ Begins a new section data block $
$ name: section name $
$ $
$ $
$ $
$ $
$ $
$ $
$ _CLASSIFICATION23 epsN epsM2p epsM2m epsM3p epsM3m $
$ Limiting values of eps=sqrt(235/fy) bounding $
$ from class2 to class 3 behaviour $
$ epsN : simple compression eps limiting value; $
$ epsM2p: positive bending M2 eps lim. value; $
$ epsM2m: negative bending M2 eps lim. value; $
$ epsM3p: positive bending M3 eps lim. value; $
$ epsM3m: negative bending M3 eps lim. value; $
$ $
$ $
$ _CLASSIFICATION34 epsN epsM2p epsM2m epsM3p epsM3m $
$ Limiting values of eps=sqrt(235/fy) bounding $
$ from class3 to class 4 behaviour $
$ epsN : simple compression eps limiting value; $
$ epsM2p: positive bending M2 eps lim. value; $
$ epsM2m: negative bending M2 eps lim. value; $
$ epsM3p: positive bending M3 eps lim. value; $
$ epsM3m: negative bending M3 eps lim. value; $
$ $
$ _FIXEDCLASS class $
$ Section will be computed according to this $
$ section classification, no matter limiting eps $
$ values. If class is 0 no forcing class will be $
$ defined (and eps values will be used) $
$ $
$ $
$ $
$ _EFFECTIVE fd Aeff W2effp W2effm W3effp W3effm De2 De3 $
$ fd: design stress for this data $
$ Aeff: effective area $
$ W2effp: effective section modulus for M2 > 0 $
$ W2effm: effective section modulus for M2 < 0 $
$ W3effp: effective section modulus for M3 > 0 $
$ W3effm: effective section modulus for M3 < 0 $
$ De2: shift in neutral axis (axis 3 direction) $
$ De3: shift in neutral axis (axis 2 direction) $
$ material fy must match the fy described here $
$ more than one _EFFECTIVE card may be added, at $
$ different fy values. $
$ $
$ _ELASTICPOINT x2i x3i At22 At32 W12 At23 At33 W13 $
$ used when section is in class 3 $
$ W2i = J2 / x3i $
$ W3i = J3 / x2i $
$ sigma = N/A + M2/W2i + M3/W3i $
$ tau2 = T2/At22 + T3/At32 + M1/W12 $
$ tau3 = T2/At23 + T3/At33 + M1/W13 $
$ tau = sqrt(tau2^2 + tau3^2) $
$ Von Mises = sqrt(sigma^2 + 3tau^2) $
$ if a modulus is null, related stress is 0 $
$ all moduli have sign, generally $
$ _SHEAR av2 av3 w2plAv2 w2plAv3 w3plAv2 w3plAv3 $
$ shear plastic moduli (6.2.6) $
$ T,2,pl,Rd= Av2*(fy / 1.732 / gammaM0) < T2,Ed $
$ T,3,pl,Rd= Av2*(fy / 1.732 / gammaM0) < T3,Ed $
$ av2 = Av2 / A $
$ av3 = Av3 / A $
$ w2pl,Av2 = W2pl,Av2 / W2pl $
$ w2pl,Av3 = W2pl,Av3 / W2pl $
$ w3pl,Av2 = W3pl,Av2 / W3pl $
$ w3pl,Av3 = W3pl,Av3 / W3pl $
$ $
$ _TORSION W1pl a $
$ torsion plastic moduli $
$ M1,plRd= W1pl * (fy / 1.732 / gammaM0) $
$ a: see 6.26 where a=1.25. 6.26 will be used to $
$ compute reduced shear resistance due to $
$ torsion. $
$ _PLASTICDOMAIN kind datum1 datum2 datum3 datum4 datum5 $
$ datum6 datum7 datum8 datum9 datum10 $
$ datum11 datum12 datum13 datum14 datum15 $
$ datum16 datum17 datum18 datum19 datum20 $
$ only used if class is 1 or 2 $
$ kind: plastic domain kind $
$ 1 linear, no datum used equation 6.2 $
$ 2 data meaning in manual, equation 6.41 $
$ $
$ _BUCKLCURVE alpha2 alpha3 $
$ imperfection factors for axis 2 and axis 3 $
$ buckling, respectively. Values different from $
$ those in the norm are allowed (e.g. alpha2=0.9)$
$ curve a0->0.13;a->0.21;b->0.34;c->0.49;d->0.76 $
$ $
$ _LATERALTORSIONAL axis radius alfaLT kfl W Iw $
$ $
$ axis: may be 2 or 3. Bending around this axis $
$ causes lateral torsional buckling. $
$ radius: kc*Lc/radius = lambda,f (6.3.2.4) $
$ compressed part whose buckling causes $
$ lateral torsional buckling (if,z) $
$ alphaLT:imperfection factor for LT $
$ kfl: see 6.3.2.4.(2B) $
$ W: see 6.3.2.4. "Wy" $
$ Iw: warping constant. $
$ $
$ $
$ _2LATERALTORSIONAL Iz It zs zj $
$ $
$ Iz: second area moment relative to symm axis $
$ $
$ It: torsional constant $
$ $
$ zs: zct - zg (distance shear center-center) $
$ presently unused $
$ $
$ zj: non symmetry factor $
$ $
$ $
$ $
$ $
$ _TORFLEX symmetry x2 x3 Iw $
$ $
$ symmetry: maybe 0, 2, 3, or 5. $
$ 0 no symm; 2 symm axis 2; 3 symm $
$ axis 3; 5 symm axis 2 and 3 $
$ $
$ x2: axis 2 coordinate of shear center (y0)$
$ $
$ x3: axis 3 coordinate of shear center (z0)$
$ $
$ Iw: warping constant $
$ $
$ $
$ $
$ _OTHER tmax $
$ $
$ tmax: maximum cross section thickness $
$ $
$ $
$ _ENDSHAPE end of section block $
$ $
$ $
$ $
$ $
$ Copyright (c) by Castalia srl - Italy - www.castaliaweb.com $
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
$
_UNITS mm N
_EC3SHAPE IPE 500 ; section name
$
$ classification
$
_CLASSIFICATION23 1.099 0.503 0.503 0.461 0.461 ; epsN epsM2p epsM2m epsM3p epsM3m
_CLASSIFICATION34 0.994 0.336 0.336 0.994 0.994 ; epsN epsM2p epsM2m epsM3p epsM3m
_FIXEDCLASS 0 ; no matter classification class will always be this (if > 0)
$
$ effective properties
$
_EFFECTIVE 275. 11160. 1927940. 1927940. 214170. 214170. 0. 0. ; fy Aeff W2effp W2effm W3effp W3effm De2 De3
$
$ resistance checks
$
_ELASTICPOINT -100. -250. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 0. -250. 6400. 0. 55750. 0. 5100. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 100. -250. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 100. -234. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 20.1 -234. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 5.1 -213. 0. 0. 0. 0. 5100. 87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 5.1 0. 0. 0. 0. 0. 5100. 87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 5.1 213. 0. 0. 0. 0. 5100. 87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 20.1 234. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 100 234. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 100 250. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 0 250. 6400. 0. -55750. 0. 5100. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -100 250. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -100 234. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -20.1 234. 6400. 0. 55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -5.1 213. 0. 0. 0. 0. 5100. -87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -5.1 0. 0. 0. 0. 0. 5100. -87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT 0 0. 0. 0. 0. 0. 5100. -87450. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -5.1 -213. 0. 0. 0. 0. 5100. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -20.1 -234. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_ELASTICPOINT -100 -234. 6400. 0. -55750. 0. 0. 0. ; x2i x3i At22 At32 W12 At23 At33 W13
_SHEAR 0.48172 0.51828 0.70589 0.47835 0.95272 0.11218 ; av2 av3 (6.2.6) w2plAv2 w2plAv3 w3plAv2 w3plAv3
_TORSION 37772. 1.25 ; W1pl a
_PLASTICNMDOMAIN 2 1.287 -1.287 0. 0.3518 2.9063 ; kind datum1 datum2 datum3 datum4 datum5
-3.2582 2. 0. 0. 1. ; datum6 datum7 datum8 datum9 datum10
0. 0. 0. 0. 5. ; datum11 datum12 datum13 datum14 datum15
0. 1. 0. 0. 1. ; datum16 datum17 datum18 datum19 datum20
$
$ stability checks
$
_BUCKLCURVE 0.21 0.34 ; buckling curve alpha values
_LATERALTORSIONAL 2 54.46 0.49 1.1 1991673. 1.249e12 ; axis i,f,z alfa(curve) kfl W Iw
_2LATERALTORSIONAL 21416800. 892900. 0. 0. ; Iz It zs zj$
_TORFLEX 2 3.010e+001 0.000e+000 2.100e+008 ; 'symmetry', 'x2=y0', 'x3=z0', 'Iw'
_OTHER 16. ; tmax
$
_ENDSHAPE
$---------------------------------------------------------
Di seguito la descrizione del formato delle varie schede.
_____________________________________________________________________
_UNITS len for
len indica l’unità di lunghezza e può essere “mm”, “cm”, “m”, “in” “ft” “yd”
for indica l’unità di forza e può essere “N”, “daN”, “kN”, “kg”, “t”, “lb”, “kip”
Tutti i dati successivi a questa scheda saranno interpretati usando queste unità di misura o le unità di misura derivate: Se si gestisce il file attraverso l'opportuno comando di Sargon, i dati dimensionali di tutte le sezioni sono espressi nelle unità correnti del modello. L'utilizzo del comando comporta inoltre la riscrittura automatica di tutti i dati nel file EC3DATA.txt con la loro conversione in N, mm e unità derivate.
_EC3SHAPE name
Name nome del profilo (sono consentiti gli spazi). Il nome non può essere più lungo di 19 caratteri
Questa scheda apre il blocco di dati relativo ad un profilo. Se si gestisce il file attraverso l'opportuno comando di Sargon, questa scheda viene compilata automaticamente in base al nome della sezione scelta.
_ENDSHAPE
Questa scheda chiude il blocco di dati relativo a un profilo. Se si gestisce il file attraverso l'opportuno comando di Sargon, questa scheda viene compilata automaticamente.
_CLASSIFICATION23 epsN epsM2p epsM2m epsM3p epsM3m
epsN numero reale
epsM2p numero reale
epsM2m numero reale
epsM3p numero reale
epsM3m numero reale
Questa scheda, gestita dalla property page Classificazione, definisce i valori limite che la ε del materiale deve soddisfare per considerare il profilo in classe 2, sotto l’azione di: una compressione semplice (epsN); un momento M2 positivo (epsM2p); un momento M2 negativo (epsM2m); un momento M3 positivo (epsM3p); un momento M3 negativo (epsM3m). Ricordiamo qui la definizione di ε:

dove fy è la tensione di snervamento del materiale adottato in N/mm2. Se risulta ε minore dei valori di soglia indicati allora la classe associata al tipo di sollecitazione indicato è la 3, altrimenti la classe è assunta pari a 2.
_CLASSIFICATION34 epsN epsM2p epsM2m epsM3p epsM3m
epsN numero reale
epsM2p numero reale
epsM2m numero reale
epsM3p numero reale
epsM3m numero reale
Questa scheda, gestita dalla property page Classificazione, definisce i valori limite che la ε del materiale deve soddisfare per considerare il profilo in classe 3, sotto l’azione di: una compressione semplice (epsN); un momento M2 positivo (epsM2p); un momento M2 negativo (epsM2m); un momento M3 positivo (epsM3p); un momento M3 negativo (epsM3m). Ricordiamo qui la definizione di ε:

dove fy è la tensione di snervamento del materiale adottato in N/mm2. Se risulta ε minore dei valori di soglia indicati allora la classe associata al tipo di sollecitazione indicato è la 4, altrimenti la classe è assunta pari a 3.
_FIXEDCLASS class
class numero compreso tra 0 e 4.
Questa scheda, gestita dalla property page Classificazione, forza il verificatore a classificare il profilo con una certa classe, indicata dal numero, indipendentemente dalle sollecitazioni applicate e/o dal materiale utilizzato. Se il numero è 0 tale opzione non risulta attivata.
_PLASTICNMDOMAIN kind datum1 datum2 datum3 datum4 datum5
datum6 datum7 datum8 datum9 datum10
datum11 datum12 datum13 datum14 datum15
datum16 datum17 datum18 datum19 datum20
kind 1 dominio lineare, 2 dominio non lineare
datum1 A parametro reale
datum2 B parametro reale
datum3 C parametro reale
datum4 D parametro reale
datum5 E parametro reale
datum6 F parametro reale
datum7 G parametro reale
datum8 H parametro reale
datum9 I parametro reale
datum10 L parametro reale
datum11 M parametro reale
datum12 N parametro reale
datum13 O parametro reale
datum14 P parametro reale
datum15 Q parametro reale
datum16 R parametro reale
datum17 S parametro reale
datum18 T parametro reale
datum19 U parametro reale
datum20 V parametro reale
Questa scheda é gestita dalla property page Valori plastici (1).
Se kind è eguale a 1 la verifica di resistenza viene condotta con un dominio limite semplificato lineare del tipo:
![]()
Se invece kind è eguale a 2, allora la verifica è di questo tipo:

n= N / Npl,Rd
MN,2,Rd=Mpl,2,Rd x [ A + Bn + Cn2]
MN,3,Rd=Mpl,3,Rd x [ D + En + Fn2]

Dove i parametri da A a V (in tutto 20) devono essere stabiliti dall’utente.
_SHEAR av2 av3 av2' av3' w2plav2' w2plav3' w3plav2' w3plav3'
av2 rapporto tra il modulo di resistenza al taglio V2 e l’area totale: av2= Av2/A
av3 rapporto tra il modulo di resistenza al taglio V3 e l’area totale: av3= Av3/A
av3' rapporto tra l'area resistente al taglio V2 e l’area totale: av2= Av2'/A (solo NTC)
av3' rapporto tra l'area resistente al taglio V3 e l’area totale: av3= Av3'/A (solo NTC)
| w2plav2' | rapporto tra il modulo di resistenza plastico per flessioni attorno all’asse 2 dell’area resistente a taglio Av2' ed il modulo di resistenza plastico complessivo: w2plAv2'= W2plAv2'/Wpl2 |
| w2plav3' | rapporto tra il modulo di resistenza plastico per flessioni attorno all’asse 2 dell’area resistente a taglio Av3' ed il modulo di resistenza plastico complessivo: w2plAv3'= W2plAv3'/Wpl2 |
| w3plav2' | rapporto tra il modulo di resistenza plastico per flessioni attorno all’asse 3 dell’area resistente a taglio Av2' ed il modulo di resistenza plastico complessivo: w3plAv2'= W3plAv2'/Wpl3 |
| w3plav3' | rapporto tra il modulo di resistenza plastico per flessioni attorno all’asse 3 dell’area resistente a taglio Av3' ed il modulo di resistenza plastico complessivo: w3plAv3'= W3plAv3'/Wpl3 |
Nota: Av è il modulo di resistenza al taglio indicato sia nell'EN1993-1-1 che nelle NTC: ad Av corrisponde, nel file EC3data.txt, il valore adimensionalizzato av. Nelle NTC viene inoltre utilizzato il simbolo Av* che è l'area resistente al taglio, cioè quella porzione dell'area totale fisicamente coinvolta nella resistenza a taglio, utilizzata nelle verifiche con sollecitazioni miste. Poichè nelle NTC ad Av* corrisponde il valore adimensionalizzato av senza asterisco, qui già utilizzato come adimensionalizzazione di Av, nel file EC3data.txt si è scelto di utilizzare questa convenzione: i simboli presenti solo nelle NTC sono indicati con l'apostrofo; nella tabella seguente sono riportate le corrispondenze tra i simboli adottati nel file EC3data.txt e quelli riportati nelle normative.
Significato |
EC3data.txt |
Eurocodice |
NTC |
modulo resistente a taglio |
Av |
Av |
Av |
modulo res. a taglio diviso area totale |
av |
non definito |
non definito |
area resistente a taglio |
Av' |
- |
Av* |
area res. a taglio diviso area totale |
av' |
- |
av |
Questi termini consentono di eseguire una verifica di resistenza in ambito plastico. I moduli di resistenza a taglio e le aree resistenti a taglio si ottengono dai corrispondenti numeri adimensionali moltiplicandoli per l’area del profilo. I termini wiplavi' possono essere posti, a favore di sicurezza, eguali ad 1 (la riduzione del modulo plastico viene fatta su tutta la sezione). Verifiche più raffinate possono essere condotte assegnando a questi numeri il loro reale valore. In questo modo il depauperamento dovuto alla presenza del taglio non verrà associato alla intera sezione ma solo alla area di taglio associata al taglio considerato. Tale regola è coerente con quella prescritta in Eurocodice, che richiede di assumere una tensione di snervamento ridotta (1-ρ)fy per l’area di taglio. Questa scheda é gestita dalla property page Valori plastici (2).
W1pl è il modulo di resistenza plastico a torsione
| a | è il numero reale che compare nella formula 6.26 di normativa con il valore 1,25. Può essere posto eguale a 1 a favore di sicurezza |
Questa scheda é gestita dalla property page Valori plastici (2) e consente di eseguire le verifiche a torsione e di valutare (tramite a) il taglio ridotto a causa della presenza della torsione.
_ELASTICPOINT x2i x3i At22 At32 W12 At23 At33 W13
X2i coordinata x2 del punto i considerato
X3i coordinata x3 del punto i considerato
At22 modulo resistente a taglio per taglio V2, direzione 2: τ2= V2/At22
At32 modulo resistente a taglio per taglio V3, direzione 2: τ2= V3/At32
W12 modulo resistente a torsione, direzione 2: τ2= M1/W12
At23 modulo resistente a taglio per taglio V2, direzione 3: τ3= V2/At23
At33 modulo resistente a taglio per taglio V3, direzione 3: τ3= V3/At33
W13 modulo resistente a torsione, direzione 3: τ3= M1/W13
Questi moduli di resistenza, in generale dotati di segno, vengono impiegati per le verifiche di resistenza di profili considerati in classe 3. Quando il modulo di resistenza è nullo è nulla anche la corrispondente tensione. Le verifiche di resistenza vengono condotte sommando tutte le τ in una direzione, le τ nell’altra direzione, calcolando la τ risultante ed infine applicando la formula di Von Mises. Questa scheda é gestita dalla property page Valori elastici.
_EFFECTIVE fd Aeff W2effp W2effm W3effp W3effm De2 De3
fd tensione di progetto da associare ai dati forniti nel seguito (fy/γM0)
Aeff area efficace
W2effp modulo di resistenza per flessioni attorno all’asse 2 momento positivo
W2effm modulo di resistenza per flessioni attorno all’asse 2 momento negativo
W3effp modulo di resistenza per flessioni attorno all’asse 2 momento positivo
W3effm modulo di resistenza per flessioni attorno all’asse 2 momento negativo
De2 traslazione del baricentro sotto azione assiale di compressione ΔM2=NxDe2
De3 traslazione del baricentro sotto azione assiale di compressione ΔM3=NxDe3
Questa scheda, gestita dalla property page Valori efficaci, definisce le caratteristiche efficaci ed è tipicamente da usare per le verifiche di sezioni in classe 4. Perché il programma possa verificare, la tensione di snervamento indicata deve effettivamente corrispondere a quella associata alla sezione indicata nel modello all’esame. Si noti che il programma usa una formula lievemente diversa da quella di normativa in quanto associa ciascun modulo efficace al segno della corrispondente azione flettente, tenendo quindi conto del fatto che il modulo efficace può mutare invertendo il segno della sollecitazione flettente.
alpha2 parametro di imperfezione associato allo sbandamento per flessioni attorno all’asse 2
alpha3 parametro di imperfezione associato allo sbandamento per flessioni attorno all’asse 3
Questi parametri di imperfezione devono valere:
0,13 per la curva a0
0,21 per la curva a
0,34 per la curva b
0,49 per la curva c
0,76 per la curva d
Questa scheda é gestita dalla property page Instabilità e determina le verifiche a stabilità (escluso lo svergolamento).
Il programma consente, tuttavia, anche di specificare valori diversi da questi, ove specifiche esigenze di verifica lo richiedano. Il parametro di imperfezione può essere definito mediante un valore intermedio tra quelli di due curve o maggiore di quello della curva d. Si sconsiglia di adoperare valori non normati se non si è ben certi di ciò che si sta facendo.
_LATERALTORSIONAL axis i,f,z alphaLT kfl W Iw
Axis può valere 2 o 3: è l’asse di flessione che causa lo svergolamento
Ifz è il raggio di inerzia della piattabanda compressa
alphaLT è il fattore di imperfezione della curva di stabilità da adottare
kc=kfl è un coefficiente che mitiga la severità della verifica
| W | è il modulo di resistenza da associare alla flessione per il calcolo della tensione di compressione nella piattabanda compressa |
| Iw | è la costante di ingobbamento |
Nella verifica a svergolamento le sezioni utente utilizzano il metodo della piattabanda equivalente compressa (par. 6.3.2.4. della norma). Tutti i dati forniti in questa scheda servono a questa verifica ad eccezione della costante di ingobbamento che serve per valutare NcrT nella formula per CmLT del metodo 1 (cfr. tabella A.1). E’ possibile porre un valore 0 per la costante di ingobbamento. Questa scheda é gestita dalla property page Instabilità.
_2LATERALTORSIONAL Iz It zs zj
Iz il momento di inerzia attorno all'asse di simmetria
It il momento di inerzia torsionale
zs zct - zg
zj indice di non simmetria
Questi dati, gestiti dalla property page Instabilità, servono a calcolare il momento critico secondo la formula canonica per sezioni aventi un asse di simmetria (cfr. ad esempio ENV 1993-1-1 appendice F, [F2]). In effetti, se e solo se viene aggiunta la scheda "_2LATERALTORSIONAL", allora il momento critico non verrà calcolato con il metodo della piattabanda compressa, bensì con la formula teorica seguente:

nella quale Iz, It, e zj sono letti nella scheda "_2LATERALTORSIONAL", mentre Iw è letto nella scheda "_LATERALTORSIONAL". k è il β1. Si è fatta l'ipotesi che il carico sia applicato nel centro di taglio (zg=0) e che C3 sia eguale ad 1. E' da notare che le quantità Iw e zj sono fornite da Sargon per alcune forme sezionali (bottone Dettagli del dialogo della forma sezionale formata a freddo ) e dovranno essere riportate manualmente nel file EC3DATA.TXT. In caso di doppia simmetria zs e zj sono nulli. L'asse attorno al quale la flessione provoca lo svergolamento è specificato nella scheda "LATERALTORSIONAL" e può essere il 2 o il 3. Se nonostante sia presente la scheda "_2LATERALTORSIONAL" non si vuole calcolare il momento critico con la formula canonica, ma usare il metodo della piattabanda compressa, basta porre eguale a zero Iz o It.
symmetry codice che dice se la sezione è simmetrica. 0: non simmetrica; 2: simmetrica rispetto all'asse 2; 3 simmetrica rispetto all'asse 3; 5 doppiamente simmetrica (assi 2 e 3). Si ricorda che asse 2 = asse y; asse 3: asse z.
y0 distanza con segno tra il baricentro e il centro di taglio lungo l'asse 2 (asse y).
z0 distanza con segno tra il baricentro e il centro di taglio lungo l'asse 3 (asse z).
Iw costante di ingobbamento
Questi dati, gestiti dalla property page Instabilità, servono a calcolare l'azione assiale critica per instabilità torsionale (T) o torsoflessionale (TF) secondo la formula canonica per sezioni aventi un asse di simmetria (cfr. ad esempio EN 1993-1-3, e si veda la sezione dedicata alle verifiche a instabilità torsionale e flesso-torsionale). In effetti, se e solo se viene aggiunta la scheda "_TORFLEX", allora l'azione assiale critica Ncr,T verrà calcolata, altriementi no. Essa non verrà calcolata anche nel caso in cui symmetry = 0. In tal caso le verifiche a instabilità per azione assiale terranno conto solo della instabilità flessionale (euleriana).
Il carico critico Ncr,T viene calcolato con con la formula teorica seguente:
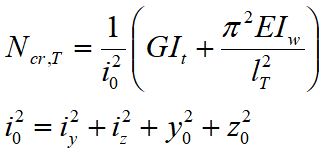
nella quale y0, z0, e Iw sono letti nella scheda "_TORFLEX". I raggi di inerzia iy ed iz si riferiscono agli assi principali 2 e 3 rispettivamente (iy=i2, iz=i3). It è il momento di inerzia torsionale primario e lT è identica alla lunghezza di libera inflessione per svergolamento, dominata dal coefficiente β1.
Se la simmetria è doppia (symmetry = 5) allora Ncr,TF = Ncr,T. In caso contrario, nella ipotesi in cui l'asse di simmetria sia l'asse y (o asse principale 2), la formula per Ncr,TF è la seguente:

nella quale Ncr,y è il carico critico per instabilità flessionale attorno all'asse y (asse 2, di simmetria). Si noti che se y (2) è di simmetria allora z0=0.
Se invece la simmetria è relativa all'asse z (o asse 3, symmetry = 3), le formule diventano le seguenti:

| tmax | spessore massimo dei piatti costituenti il profilo |
Questo dato, gestito dalla property page Altro, consente se necessario di ridurre la tensione di snervamento del materiale (spessori maggiori di 40mm).
_____________________________________________________________________
5.3 Esempio di aggiunta di una sezione al file: IPE500
IPE500
h=500mm
b=200mm
tw=10.2mm
tf=16mm
r=21mm
A= 11552mm2
J2= 481985120mm4
J3= 21416800 mm4
Wpl2= 2194120 mm3
Wpl3= 335880 mm3
Classificazione
Flangia
c/tf= (200-10.2-21-21)*0.5/16 = 4.61
In compressione:
epsN23= (c/tf)/10=0.461
epsN34= (c/tf)/14=0.329
In flessione M2
epsM223= (c/tf)/10=0.461
epsM234= (c/tf)/14=0.329
In flessione M3
epsM323= (c/tf)/10=0.461
epsM334= (c/tf)/14=0.329
Anima
c/tw= (500-32-42)/10.2=41,76
In compressione:
epsN23= (c/tw)/38=1.099
epsN34= (c/tw)/42=0.994
In flessione M2
epsM223= (c/tw)/83=0.503
epsM234= (c/tw)/124=0.336
In flessione M3
Indefinito
Pertanto concludo
epsN23=max(0.461, 1.099)=1.099
epsM223=max(0.461, 0.503)=0.503
epsM323=max(0.461, -)=0.461
epsN34=max(0.329, 0.994)=0.994
epsM234=max(0.329, 0.336)=0.336
epsM334=max(0.329, 0.994)=0.994
Pertanto
Se ε > 1.099 classe in compressione N 2 o 1
Se ε > 0.503 classe in flessione M2 2 o 1
Se ε > 0.461 classe in flessione M3 2 o 1
Se ε > 0.994 classe in compressione N 3
Se ε > 0.336 classe in flessione M2 3
Se ε > 0.994 classe in flessione M3 3
Se ε < 0.994 classe in compressione N 4
Se ε < 0.336 classe in flessione M2 4
Se ε < 0.994 classe in flessione M3 4
Caratteristiche efficaci (S275)
?=eps = sqrt(235/275)=0.924
Classe in compressione: 4 De2=De3=0
Classe per M2: 1
Classe per M3: 4
Sotto azione assiale e momento M3 l’anima si parzializza nel tratto centrale per una lunghezza pari a bneff=mm. Sotto M2 il profilo resta interamente reagente. Quindi sotto M2 i W efficaci coincidono con quelli elastici. La variazione di W sotto M3 è trascurabile (perché la parzializzazione riguarda l’anima). Resta pertanto da calcolare l’area efficace per sottrazione. Non vi è spostamento di baricentro in questo caso.
kσ=4

![]()
hneff=(1-0,9092)426=38,68
Aeff= A –twhneff=11552 – 10,2x38,68=11157mm2.
W2effp= W2effm= W2=1 927 940 mm3.
W3effp= W3effm =W3= 214 170 mm3.
Punti elastici

Il calcolo dei moduli di resistenza viene eseguito in 21 punti come da immagine allegata.
Per quanto riguarda la flessione il programma chiede le coordinate rispetto al sistema di riferimento principale tenendo presente che x2 è misurata lungo l’asse 2 (e quindi corrisponde alla y dei disegni in Eurocodice 3) mentre x3 è misurata lungo l’asse 3 e quindi corrisponde alla z dei disegni dell’Eurocodice 3.
Per il taglio si invoca una redistribuzione (cosa consentita) e quindi si assume una ? diretta come l’asse 2 e costante sulle ali, diretta come l’asse 3 e costante nell’anima. Il modulo di resistenza è dato dalla somma delle aree delle ali e dall’area dell’anima (con l’altezza totale).
Per la torsione si ipotizza una distribuzione lineare nello spessore con valore nullo nel punto medio dello stesso spessore. Il modulo di resistenza di un piatto di spessore t si ottiene da Jt/t, e quindi per l’anima 892900/10.2=87450mm3, mentre per le ali 892000/16=55750mm3.
I segni dipendono dal corrispondente segno della tensione nel sistema di riferimento principale. Sono positive le trazioni e le tensioni tangenziali nel verso positivo degli assi.
In definitiva la tabella dei numeri da introdurre è la seguente (tutti i dati in mm, mm2 o mm3):
Punto |
X2i |
X3i |
At22 |
At32 |
W12 |
At23 |
At33 |
W13 |
|---|---|---|---|---|---|---|---|---|
1 |
-100 |
-250 |
6400 |
0 |
55750 |
0 |
0 |
0 |
2 |
0 |
-250 |
6400 |
0 |
55750 |
0 |
5100 |
0 |
3 |
100 |
-250 |
6400 |
0 |
55750 |
0 |
0 |
0 |
4 |
100 |
-234 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
5 |
20.1 |
-234 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
6 |
5.1 |
-213 |
0 |
0 |
0 |
0 |
5100 |
87450 |
7 |
5.1 |
0 |
0 |
0 |
0 |
0 |
5100 |
87450 |
8 |
5.1 |
213 |
0 |
0 |
0 |
0 |
5100 |
87450 |
9 |
20.1 |
234 |
6400 |
0 |
55750 |
0 |
0 |
0 |
10 |
100 |
234 |
6400 |
0 |
55750 |
0 |
0 |
0 |
11 |
100 |
250 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
12 |
0 |
250 |
6400 |
0 |
-55750 |
0 |
5100 |
0 |
13 |
-100 |
250 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
14 |
-100 |
234 |
6400 |
0 |
55750 |
0 |
0 |
0 |
15 |
-20.1 |
234 |
6400 |
0 |
55750 |
0 |
0 |
0 |
16 |
-5.1 |
213 |
0 |
0 |
0 |
0 |
5100 |
-87450 |
17 |
-5.1 |
0 |
0 |
0 |
0 |
0 |
5100 |
-87450 |
18 |
0 |
0 |
0 |
0 |
0 |
0 |
5100 |
-87450 |
19 |
-5.1 |
-213 |
0 |
0 |
0 |
0 |
5100 |
0 |
20 |
-20.1 |
-234 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
21 |
-100 |
-234 |
6400 |
0 |
-55750 |
0 |
0 |
0 |
Aree di taglio (per il calcolo plastico)
Per questo profilo in accordo all’Eurocodice 3 si ha:
Av3=11552 – 2 *200 * 16 +(10,2 + 2*21)*16=5987,2 mm2.
Per quanto riguarda l’are per taglio parallelo alle ali, in mancanza di specificazioni:
Av2=11552 – 5987,2= 5564,8mm2.
Da cui
av2= 5564,8/11552=0,48172
av3=0,51828
Il calcolo dei w viene eseguito ipotizzando che Av2 coincida con le ali ed Av3 coincida con la quantità definita dalla norma come (A-2btf+(tw+2r)tf) ovvero la sezione totale depurata dei quattro monconi d’ala di area (0,5b-0,5tw-r)tf.
w2,pl,Av2= 2x200x16x(250-8)/2194120=0,70589
w2,pl,Av3= [2194120-2x16x(200-2x21-10,2)x(250-8)]/2194120=0,47835
w3,pl,Av2= 2x200x16x(200/4)/335880=0,95272
w3,pl,Av3= [335880-4x16x(100-5,1-21)(50+2,55+10,5)]/335880=0,11218
Si noti come tali valori risultino, anche talvolta significativamente, minori di 1.
Torsione (per il calcolo plastico)
Il momento resistente plastico può essere ottenuto da:
M1pl = 2x200x16x[fy/sqrt(3)]x16/4 + (500-16x2)x10,2 x[fy/sqrt(3)]x10,2/4=37772[fy/sqrt(3)]
E quindi
W1pl = 37772mm3
Dominio plastico
Calcolo dei momenti ridotti
Il modello è
MN,i,Rd=Mpl,i,Rd x [ A + Bn + Cn2]
Dove per definizione
n= N / Npl,Rd
Nel caso dei profili IPE si sposa la formula di normativa ponendo:
per i=y=asse2:
(1-n)/(1-0,5a)= [ A + Bn + Cn2]
Essendo
a= (A-2btf)/A=(11552 – 2 * 200 * 16) / 11552 = 0.446
E quindi
A= 1 / (1-0,5a)=1,287
B= -1 / (1-0,5a)=-1,287
C=0
Per i=z=asse 3
1-[(n-a)/(1-a)]2=[ D + En + Fn2]
E con un pò di conti si vede che deve essere
D= (1-2a)/ (1-a)2= 0,3518
E= 2a/(1-a)2= 2,9063
F= -1/ (1-a)2=-3,2582
Determinazione di α e β
Il modello prevede (6.41):

Nel caso di una ipe 500 deve essere
α=2
β=5n > 1
E quindi:
G=2
H=0
I=0
L=1
M=0
N=0
O=0
P=0
Q=5
R=0
S=1
T=0
U=0
V=1
Curve di stabilità
Curva per asse 2: a α=0.21
Curva per asse 3: b α =0.34
Comportamento a svergolamento
Si assume il raggio di inerzia della piattabanda compressa.
h1= 500 – 16x2-21x2= 426
If= 0,5*[I3 – (1/12)(10,23*426]=0,5*[ I3-37672,9]= 0,5*[ 21416800-37672,9]=10 689 563 mm4.
Af=0,5*(11552 – 426*10,2)=3603,4
if= sqrt(10 689 563 / 3603,4) = 54,46mm
Come curva di stabilità si adotta la curva c e quindi αLT=0.49
Il coefficiente riduttivo kfl (6.3.2.4.(2)) viene posto eguale a 1,1.
Il modulo di resistenza della flangia si ottiene moltiplicando il modulo di resistenza della sezione per il rapporto tra la semialtezza ed il braccio ridotto:
W= 1927940x250/(250-8)= 1991673
La costante di ingobbamento è pari a:
Iw= 1,249 x 1012mm6
____________________________________________________________________________
6 Il tracciamento dei calcoli
Data la complessità dei calcoli da eseguire e le differenti possibili strategie di calcolo possibili, il verificatore è stato dotato di una importante funzionalità che consente di “tracciare” i calcoli svolti, ottenendo un file nel quale non solo gli indici di sfruttamento ma anche tutti i risultati intermedi siano disponibili (vedasi il dialogo opportuno). La funzionalità va intesa come uno strumento aggiuntivo da impiegare in casi particolari. In alternativa è possibile, a prezzo di tabulati anche molto estesi e di tempi di calcolo sensibilmente superiori, produrre il tabulato come ulteriore documentazione del lavoro.
Il tracciamento produce un file con nome “modello.eur.txt” che usa imprescindibilmente i N ed i mm come unità di misura (nonché le unità derivate).
7 L’uso di checksolvers
Il programma checksolvers è stato ampliato per consentire di eseguire controlli di elaborazione anche sul verificatore in accordo all’Eurocodice 3. Le nuove schede sono:
_TRESCOM TNUM CASE KIND TARGET
_TSTACOM TNUM CASE KIND TARGET
_BRESCOM BNUM CASE KIND TARGET
_BSTACOM BNUM CASE KIND TARGET
In cui CASE è il numero della combinazione, BNUM e TNUM sono il numero di elemento, KIND è il tipo di controllo (generalmente “CROSS”) e TARGET è il numero obiettivo. La scheda TRESCOM va a leggere il valore del massimo indice di sfruttamento a resistenza per elementi truss nella combinazione considerata; la scheda BRESCOM fa lo stesso ma per elementi beam. La scheda BSTACOM va a controllare l’indice di sfruttamento a stabilità per elementi beam. La scheda TSTACOM lo fa per elementi truss.
Tale funzionalità è molto importante poiché consente, ad ogni versione, di eseguire delle verifiche sulla bontà della elaborazione su un certo gruppo di casi test che siano stati messi a punto. Anche ciascun utente può, a sua discrezione, mettere a punto casi di prova.
Castalia srl ha messo a punto circa 100 casi test sul verificatore in accordo ad Eurocodice 3. Tali casi test sono consegnati insieme con il programma. La determinazione dei valori obiettivo è stata fatta con un lungo e attento lavoro che è confluito nelle schede di validazione.
8 Le schede di validazione
Il lavoro di sviluppo e di attento studio della normativa ha portato, tra l’altro, alla creazione di ben 100 schede di validazione, ovvero alla analisi di 100 diverse situazioni di progetto e verifica relative sia alla resistenza che alla stabilità. Tale lavoro rappresenta un risultato di primissima importanza poiché costituisce una messe considerevole di dati a disposizione sia degli utenti che di un pubblico più ampio (ad esempio i Clienti degli utilizzatori del programma). Ad oggi non risulta siano disponibili schede di questo tipo relative alla norma EN 1993, per lo meno in Italia.
Ben consapevoli della importanza della messa a punto di un simile insieme di test (i quali tra l’altro hanno consentito di approfondire notevolemente il testo della norma, nonché di coglierne numerosi limiti) si è deciso di far afferire queste 100 schede di validazione all’interno di una vera e propria pubblicazione ([2]). Per questo motivo, sino alla pubblicazione di dette schede all’interno di tale pubblicazione, queste schede di validazione non sono inserite nella documentazione del programma: esse saranno rese disponibili all’interno della documentazione del programma una volta che siano state ufficielmente pubblicate.
Al momento le schede disponibili sono 100, delle quali 50 si riferiscono a verifiche di resistenza e 50 a verifiche a stabilità. Sono indagati sia il metodo 1 che il metodo 2 con una vasta gamma di profili. Ogni scheda presenta i dati di partenza, alcuni dei più importanti dati intermedi e gli indici di sfruttamento finali, così come sono stati calcolati a mano o mediante fogli Excel. Questi risultati sono poi comparati, con pieno successo, con quelli forniti dal programma. Non appena la paternità del lavoro non potrà più essere oggetto di discussione, e quindi dopo la pubblicazione formale, le schede saranno anche posizionate nel sito internet di Castalia.
Bibliografia
[1] Rugarli P. “La classificazione delle sezioni. Commento ad Eurocodice 3”, EPC LIBRI, 2007
[2] Rugarli P. “Software di calcolo di travi in accordo ad EN1993-1-1”, EPC LIBRI, 2008 (in stesura)
[3] Rugarli P. “Commento generale ad Eurocodice 3”, EPC LIBRI, 2008 (in stesura)
[4] ECCS “Rules for Member Stability in EN 1993-1-1, background documentations and design guidelines”, N°119, 2006
[5] Rondal J., Wurker K.G., Dutta D. “Structural stability of hollow sections”, Verlag TUV Rheinland, 1992
[6] M.A. Serna, A.Lopez et al. “Equivalent uniform moment factors for lateral-torsional buckling of steel members”, Journal of Constructional Steel Research, 62, 566-580, 2006
________________________________________________________________________
VERSIONE ENV (NON PIÙ RILASCIATA A PARTIRE DAL NOVEMBRE 2007).
L'eurocodice 3 (EC3) si preannuncia come la normativa di riferimento dei prossimi anni. Di seguito verranno date informazioni utili alla comprensione di quanto eseguito dal programma e di quanto da esso stampato, dando per scontata la conoscenza della Norma.
Si tenga presente che la relativa provvisorietà dell'EC3 rende possibili aggiornamenti o modifiche anche di non lieve entità (tal modifiche, si ritiene, si renderanno specialmente necessarie nell'ambito della classificazione).
L'ampiezza e la complessità della norma rendono impossibile, in quest'ambito, la completa descrizione di tutti gli aspetti specifici. In queste note verranno quindi richiamati i principali aspetti d'interesse, fermo restando che Castalia è a disposizione dei propri clienti con diritto all'aggiornamento, per tutte le spiegazioni che si rendessero necessarie.
Sono stati implementati i seguenti paragrafi dell' EC3:
5.1.1.
5.3
5.4.1
5.4.2.
5.4.3.
5.4.4.
5.4.5.
5.4.6.
5.4.7.
5.4.8.
5.4.9.
5.5.1.
5.5.2.
5.5.3.
5.5.4.
5.6.1.
5.6.2.
5.6.3.
5.6.7.
annesso F.
Particolare rilievo, nell'ambito del codice così come nell'ambito della sua programmazione, ha assunto il problema della classificazione delle sezioni.
LA CLASSIFICAZIONE DELLE SEZIONI
Come chiarito in [articolo1], il problema della classificazione delle sezioni nell'ambito di uno stato di sforzo generale (due componenti di momento, una di azione assiale), è tutt'altro che banale.
SARGON risolve completamente il problema nel caso di sezioni ad I (IPE, HEA, ecc.) così come chiarito in [1], mentre relativamente agli altri profili SARGON assume come classe la massima classe tra quelle dovute a sollecitazioni pure (sola N, solo M2, solo M3). Nel caso di elementi biella SARGON assume come classe la classe 1 se l'elemento è in trazione, la classe a compressione semplice in caso contrario.
Il caso di classe 4 è da considerare un caso a sè. Il calcolo delle grandezze efficaci viene eseguito, nella versione 1.00 del verificatore, per i soli profili ad I laminati. Negli altri casi tali grandezze sono poste eguali a zero.
Un profilo che risulti di classe 4 e non sia un profilo ad I viene considerato non verificato, ed a esso è associato il coefficiente di sfruttamento convenzionale 99.
Profili che non siano doppiamente simmetrici presentano particolari problemi allorchè ci si trovi a calcolarne le grandezze efficaci. In tal caso infatti, anche sotto sollecitazioni semplici, gli assi principali della sezione efficace sono ruotati rispetto a quelli della sezione lorda, facendo con ciò perdere un pò di vista il significato delle verifiche a stabilità. In attesa di maggiori chiarimenti da parte del Normatore SARGON in tali casi non verifica il profilo.
A partire dalla versione 7.20 di Sargon i profili la cui sezione ha un nome che comincia con “CL3_” verranno forzati ad essere in classe 3 anche se per ipotesi fossero in classe 4. Ciò consente di trattare anche le sezioni saldate o laminate che debbano essere adeguatamente irrigidite, senza che queste, essendo classificate in classe 4, vengano ingiustamente penalizzate. E’ compito del progettista garantire che le travi abbiano gli irrigidimenti necessari a garantire che la classe sia effettivamente la 3. Il nome della sezione, che comincia con “CL3_” vuole far capire che si tratta di una “forzatura” rispetto ai dati puramente ideali della sezione priva di irrigidimenti.
A partire dalla versione 7.20 quando per profili classificati in accordo a quanto chiarito nell’articolo citato uno qualsiasi di questi tre rapporti, in valore assoluto
N/Npl M2/M2pl M3/M3pl
è minore di 1.e-4 (0.0001), allora la corrispondente componente di sollecitazione è assunta nulla ai fini della classificazione. Tale accorgimento evita che compressioni puramente numeriche (piccoli valori di compressione in presenza di momento nullo) possano portare a classificazioni troppo severe.
CALCOLO DELLA SNELLEZZA ADIMENSIONALE λLT
Il calcolo della snellezza adimensionale è eseguito seguendo quanto prescritto nell'annesso F. Relativamente al calcolo dei coefficienti C1, C2, e C3 va detto quanto segue. La norma non fornisce in tal caso alcuna formula chiusa per valutare questi coefficienti. Le tabelle date nella norma non sono quindi praticamente utilizzabili. Per tale motivo, in attesa di una più precisa trattazione del problema, SARGON pone a favore di sicurezza:
C1= 1
C2= 0
C3= 1
GENERAZIONE DELLE COMBINAZIONI DI CARICO
SARGON genera automaticamente le combinazioni di carico partendo dai casi di carico base. Per generare le combinazioni SARGON utilizza le informazioni sul tipo di carico date dall'utente, nonché una serie di dettagliate informazioni su vari coefficienti e sulla possibile variabilità e contemporaneità dei casi di carico base. Si rimanda a quanto chiarito in Come Generare le combinazioni ed al comando di generazione delle combiazioni Genera.
SUPERELEMENTI
I superelementi ottenuti riunendo profili diversi sono calcolati assumendo come profilo di riferimento il profilo avente area minima.
TABULATO
Nel tabulato vengono date informazioni relative alle grandezze limite definite dalla normativa. Tali grandezze possono essere calcolate nell'ipotesi di profilo in classi 1 e 2, ovvero nell'ipotesi di profilo di classe 3, o di profilo in classe 4. Nel tabulato vengono riportate le grandezze d'interesse nei vari casi. Si tenga presente che l'unica forma sezionale per la quale sono calcolate le grandezze efficaci è, nella versione 1.00 del verificatore, la sezione ad I laminata (HEA, B, M, IPE ecc.): le altre forme sezionali hanno caratteristiche efficaci poste eguali a zero.
PERSONALIZZAZIONE DEL VERIFICATORE SECONDO EC3
I coefficienti gamma relativi al materiale (γM0, γM1, γM2) possono essere modificati in un opportuno dialogo, accessibile dal dialogo che consente di impostare l’EC3 come norma attiva (Norma).