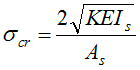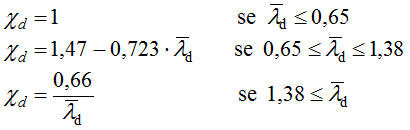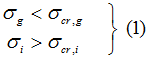Premessa
I dettagli di implementazione degli algoritmi collegati al calcolo delle grandezze efficaci sono molto complessi, e con ogni probabilità esulano dallo scopo di questa guida. A tale riguardo, si accenna al fatto che è in programma un testo monografico su questo argomento (sul calcolo delle aree efficaci) che probabimente farà seguito alla serie già pubblicata presso l'editore EPC sulle strutture in acciaio ([5], [6]).
Le informazioni che verranno date nel seguito sono soggette a copyright: possono essere utilizzate solo a patto di citare la fonte.
La esatta citazione di questo documento è la seguente:
Rugarli P.
in "Guida al programma CLASS4"
"Note in merito alla implementazione di EN 1993 per il calcolo delle aree efficaci"
Castalia srl, Milano 2011.
(http://www.castaliaweb.com/ita/p/cl4/HTML/index.html)
E' appena il caso di dire che quanto qui sarà detto per EN 1993 (Eurocodice 3) vale anche per le norme italiane NTC 2008 ([3] e [4]) che pedissequamente riportano (brandelli del) le [1], [2], e [12].
Il modello di calcolo di CLASS4
CLASS4 è un programma che utilizza un nucleo di calcolo generale, che non dipende dalla particolare tipologia sezionale introdotta. In effetti, CLASS4 non è che la versione ridotta di questo algoritmo che è stato sviluppato nell'ambito del lavoro di ricerca di Castalia srl in merito ai profili formati a freddo.
Dato che l'algoritmo è generale, non possono essere sfruttate informazioni che sono tipiche di questa o quella forma sezionale: l'algoritmo è concepito per funzionare in una vasta pluralità di casi e non può fare assegnamento su ipotesi od assunzioni ad hoc.
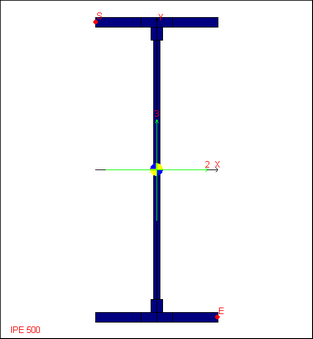
IPE 500: modello di calcolo adottato da CLASS4
L'algoritmo generale lavora su un modello di sezione così concepito: la sezione è vista come un vettore di lati curvilinei (archi di cerchio) o rettilinei, i quali possono essere o a sbalzo ("outstand") o doppiamente appoggiati ("web"). Lo spessore dei lati può anche essere diverso. Dato che non si tiene conto mediante modellazione specifica dei bulbi di raccordo per i profili laminati, questi vengono modellati mediante tratti rettilinei corti, che hanno un'area pari all'area dei raccordi curvilinei. L'effetto di tale trucco computazionale è generalmente molto modesto. La corretta lunghezza dei lati bp (sia dell'anima che delle flange) ai fini della valutazione dei rapporti larghezza spessore, è rispettata.
Il programma gestisce anche gli irrigidimenti terminali ("edge stiffener", [1]) , a patto che l'utente spieghi quali lati compongono tali irrigidimenti. Vi è una certa dose di arbitrarietà su cosa considerare come "irrigidimento" e cosa no. Un aiuto è dato dal fatto che la norma [1] specifica dei limiti del rapporto larghezza spessore al di sopra e al di sotto dei quali i lati dell'irrigidimento sono troppo lunghi o troppo corti (e quindi l'"irrigidimento" non può agire come tale). Se si scelgono lati che non rispettano i limiti di norma (par. 5.2.(2) in [1]) CLASS4 dà un messaggio di avviso. Resta tuttavia una certa ambiguità, dato che se non si qualifica come "irrigidimento" una certa parte di sezione, l'algortimo non verifica che questo possa portare la quota parte di carico assegnata e dunque non viene controllato il distorsional buckling. E' dunque compito dell'utente specificare quali lati (inclusi quelli curvi) facciano parte di un irrigidimento, non introducendo quelli che non possono essere efficaci perchè troppo corti (al punto 5.2(2) della [1] si dice infatti che se le pieghe sono troppo corte di esse non si deve tenere conto). Al punto 5.2(2) della [1] non si dice invece cosa si debba fare se le pieghe sono troppo lunghe.
Stabilita la forma sezionale di calcolo il programma procede a semplificarla ulteriormente eliminando i lati curvilinei, se presenti. Tale procedura è opzionale, ma fortemente consigliata. Se i lati curvilinei non vengono eliminati, infatti, il calcolo viene fatto facendo le seguenti ipotesi:
| 1. | I lati curvilinei non sono sede di imbozzamento e restano sempre integralmente efficaci; |
| 2. | I lati rettilinei vengono verificati all'imbozzamento locale usando la loro lunghezza nominale br al fine del calcolo dei rapporti larghezza-spessore. |
Se viceversa si decide di eliminare i lati curvilinei, allora questi vengono rettificati usando le regole di [1] (EN 1993-1-3) al par. 5.1.
In questo caso vi è una certa ambiguità di applicazione della norma, che si riscontra negli esempi disponibili in letteratura. L'argomento sarà approfondito in seguito (Il problema del computo dei gr ).
Il programma assume che la sezione lorda sia assoggettata a 5 diverse sollecitazioni elementari (per le ragioni spiegate in dettaglio più avanti), ed in ognuno di questi 5 casi arriva a valutare il modulo di resistenza pertinente della sezione efficace risultante dalla applicazione alla lorda della sollecitazione elementare. La sezione efficace è in generale completamente diversa da quella lorda: cambia il baricentro e cambiano gli assi principali (si veda più oltre). I moduli di resistenza vengono calcolati in modo che il prodotto di questi per la tensione di progetto dia luogo alla sollecitazione massima effettivamente applicabile sulla sezione efficace corrispondente alla sollecitazione elementare.
Il calcolo eseguito da CLASS4 è molto complesso, di tipo iterativo e contiene numerose assunzioni che sono frutto di anni di studio e di lavoro. E' un programma ad alto valore aggiunto. Nondimeno, i risultati che si ottengono non possono essere considerati dotati di una precisione minimamente comparabile con quella di altre procedure numeriche, di altri ambiti della ingegneria strutturale. Ciò dipende dal fatto che il metodo di calcolo indicato nelle norme (si intende le [1] e [2], "copiate" poi dalle norme [3] e [4]), è ancora molto poco preciso e soggetto (proprio a causa di questa mancanza di precisione originaria) a interpretazioni diverse e diverse applicazioni, anche all'interno del medesimo documento (si veda ad esempio [10] che denuda involontariamente le incertezze ancora presenti nei normatori).
Tra gli autori vi sono discordanze ed anche opinioni differenti. In particolare, resta molto discutibile la incoerenza tra l'esigenza di procedure molto complesse e la scarsa precisione del metodo quando si osservino i risultati sperimentali. In [8] e [9] vien fatto appunto vedere che gli errori sono ingenti (30-40%).
Relativamente al calcolo delle caratteristiche efficaci si osserva che differenze, tra i vari Autori, nell'ordine del 5% sono normali, raggiungendo talvolta anche soglie maggiori (più del 10% ad esempio in certi casi, tra [10] e [11], si veda la pagina di validazione).
Nel seguito si darà brevemente conto di alcuni problemi di implementazione, chiarendo quali sono le ragioni che fanno propendere per una scelta da parte di chi scrive.
Alcuni problemi di implementazione
A causa della difettosa scrittura della norma [1]-[2], molto probabilmente causata dalla ricerca ancora in atto sugli algoritmi di calcolo dei profili in classe 4, sono possibili varie interpretazioni del dettato normativo, le quali danno luogo a diversi possibili algoritmi, tutti contemplati dal testo attuale della norma.
A seconda che si tenga o meno conto di certe opzioni, ed a seconda che si tenga o meno conto di certe circostanze, si può pervenire a risultati diversi per il calcolo delle grandezze efficaci. Il problema riguarda tutti i profili in classe 4, ma in particolare i profili formati a freddo. Nel seguito si darà conto di alcuni di questi possibili diversi modi di applicare la norma, discutendo le conseguenze e le ragioni per propendere per una scelta o l'altra.
1) Il problema della contemporaneità delle sollecitazioni
La presenza contemporanea di 3 sollecitazioni che danno luogo a tensione normale (N, My, Mz), porta alla necessità di esaminare la sezione sotto la terna di valori (N, My, Mz) pensati agenti contemporaneamente. Dato che ciò imporrebbe un procedimento iterativo su ogni singola sezione di ogni singolo elemento in ogni singola combinazione di carico, la norma [1]-[12] fa una importante semplificazione (pur consentendo di usare il metodo più rigoroso): considera agenti separatamente le tre sollecitazioni, calcolando tra sfruttamenti elementari su tre sezioni differenti: la sezione "N" sotto l'azione assiale da sola; la sezione "My" sotto il solo My; la sezione "Mz" sotto il solo Mz. La parzializzazione dei lati compressi a causa della instabilità locale fa sì che in generale sotto ogni diverso insieme di (N, My, Mz) si abbia una sezione "efficace" diversa.
Anzichè risolvere per ogni combinazione
(N, My, Mz)--> ΩN,My,Mz
essendo ΩN,My,Mz una forma sezionale efficace, la norma consente di risolvere, una volta per tutte, i tre problemi
(N, 0, 0)--> ΩN
(0, My, 0)-->ΩMy
(0, 0, Mz)-->ΩMz
con una drastica riduzione dei tempi di calcolo (ma una drastica perdita del senso fisico del problema).
A dire il vero, tenuto conto che se N>0. ΩN+=Ω, e che la forma sezionale efficace dipende dal segno del momento applicato, di problemi occorre risolverne 5:
(N-, 0, 0)--> ΩN-
(0, My+, 0)-->ΩMy+
(0, 0, Mz+)-->ΩMz+
(0, My-, 0)-->ΩMy-
(0, 0, Mz-)-->ΩMz-
In ognuno dei casi precedenti occorre trovare la forma sezionale efficace coerente con la sollecitazione applicata, ed in particolare di queste 5 diverse forme sezionali efficaci occorre trovare le seguenti grandezze:
ΩN--->Aeff,N-, eyN-, ezN-
ΩMy+-->Wy+,eff
ΩMz+-->Wz+,eff
ΩMy--->Wy-,eff
ΩMz--->Wz-,eff
Nella norma, con un impoverimento di notazione che porta anche a qualche confusione, viene posto:
Aeff,N-= Aeff
eyN-=eNy
ezN-=eNz
Wy+,eff=Wy,eff,min
Wz+,eff=Wz,eff,min
Wy-,eff=Wy,eff,min
Wz-,eff=Wz,eff,min
ovvero non si fa capire da quali (diverse) forme sezionali efficaci derivino i moduli di resistenza e non si distingue esplicitamente (come invece occorre fare) tra W al positivo e W al negativo. Se il momento M applicato è positivo si dovrà prendere W+, se è negativo si dovrà prendere W-.
CLASS4 calcola tutte e 7 le quantità precedentemente elencate e dà il disegno di tutte e 5 le sezioni Ω coinvolte.
2) Il problema del livello di tensione iniziale fy/γM0
Il calcolo di verifica di una sezione in classe 4 parte dalla ipotesi che questa possa in almeno un punto raggiungere la tensione di progetto fy/γM0 (in trazione o compressione). Se come nel caso delle norme italiane ([3] e [4]) avviene che γM0> 1, ne consegue che la tensione massima possibile su un lato non è fy ma fy/γM0. Ciò porta ad un beneficio, sia pur generalmente minimo, nel calcolo delle caratteristiche efficaci, dato che il valore da usare al posto di ε, è
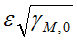
Alcuni Autori non tengono conto di questo fatto, di cui invece CLASS4 tiene conto. Ecco la ragione per cui nella videata iniziale, ed anche nel dialogo di lancio del calcolo, viene esplicitamente chiesto il valore di γM0. E' anche chiaro che a causa di questo fatto i valori efficaci cambiano a seconda non solo del tenore di acciaio usato (a causa fy) ma anche a seconda del valore di γM0 usato nel calcolo.
3) Il problema del livello di tensione σcom.sul lato in esame nel corso della iterazione
La penalizzazione di un lato ottenuta scomputando le parti non efficaci del lato stesso è tanto più severa a parità di distribuzione di tensioni (ovvero a parità di ψ) tanto più è severo il livello della tensione di compressione. La norma [2] dà dei valori di detrazione che assumono che la massima compressione sia pari ad fy. Capita tuttavia molto spesso, in specie nei problemi di flessione, che un gradiente di tensione porti ad avere lati nei quali la massima compressione σcom è minore, talvolta molto minore, di fy. In questo caso penalizzare il lato come se la sua massima compressione sia pari ad fy è troppo cattivo e porta ad una sottostima dei valori efficaci. Si noti che mentre qualche lato sulla sezione efficace avrà attinto in trazione o compressione al massimo valore di progetto di tensione, fy/γM0, non è detto che questo sia vero per tutti i lati. Per questi occorre usare al posto di
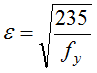
il valore
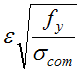
pervenendo ad aree efficaci maggiori. Infatti ciò equivale ad usare una snellezza di lato ridotta:
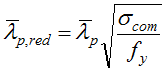
con delle formule per il calcolo di ρ lievemente diverse (2] Annex E, formule E.1 e E.2).
CLASS4 consente di scegliere se usare il livello effettivo delle tensioni ("Usa il livello effettivo delle tensioni" nel dialogo di impostazione del calcolo), oppure no.
Alcuni Autori tendono ad usare questa possibilità data dalla norma (in [2] in 4.4.(4) e in Annex E), mentre altri no. E' chiaro che i valori efficaci ottenuti cambiano.
4) Il problema della iterazione sulla forma sezionale efficace
Non appena si applicano alla sezione lorda Ω gli stress block pertinenti ad una situazione limite (attingimento della tensione di progetto in uno o più punti della sezione), è possibile che questi stress block provochino in uno o più lati un depauperamento dovuto alla inefficacia di alcune parti. Ciò dà luogo ad una nuova sezione, detta sezione efficace, Ω0. Ora, dato che gli stress block con cui si è valutata l'efficacia dei lati sono stati calcolati usando Ω e non Ω0, occorre fare una nuova iterazione, 1, per calcolare dei nuovi stress block. Nel fare questo si dovrà tener conto del fatto che, essendo in generale cambiata la posizione del baricentro, i rapporti tra le tensioni agli estremi dei lati saranno differenti, dando luogo ad un calcolo di area efficace differente alla successiva iterazione 1.
Il procedimento è quindi un procedimento iterativo e viene arrestato quando il risultato che interessa, ovvero Aeff o Weff, a seconda dei casi, muta per un valore reputato minimo. Detta D la quantità di interesse (Aeff o Weff) il procedimento di CLASS4 viene arrestato quando:
(Di+1-Di) / Di < 0,001
Non tutti gli Autori e non tutte le procedure sembrano fare uso di tale procedimento iterativo. La lettera della norma [2] fa riferimento ad un procedimento iterativo solo:
| 1. | Nel punto 4.3(4), dove però si fa cenno alla possibilità di calcolare una ΩN,My,Mz; |
| 2. | Nel punto 4.4.(4) NOTA 1, dove però si accenna al problema di σcom; |
| 3. | Nel punto E.2.(4) dove a proposito del problema dell'area efficace degli irrigidimenti si dice che il procedimento iterativo è opzionale. |
In [1] si parla di questo problema in 5.5.2.(3) dicendo che il numero minimo di passi è due dopo aver usato il verbo "may" ad indicare che tale raffinamento iterativo è opzionale.
5) Il problema della rotazione degli assi principali della sezione efficace
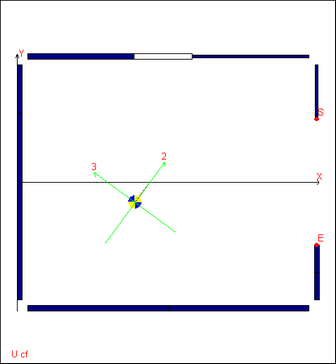
Assi principali ruotati di una sezione efficace
In CLASS4 gli assi principali sono detti "2" e "3" e non "y" e "z".
Nel precedente punto 4) si è visto che il calcolo dovrebbe essere iterativo (anche a prescindere dagli irrigidimenti ed anche usando sollecitazioni elementari). Uno dei problemi che sorgono, e dei quali non si parla molto nei veri testi disponibili (ma invece sì in [8] e [9]) è il problema della rotazione degli assi principali della sezione efficace rispetto agli assi principali della sezione lorda. CLASS4 tiene correttamente conto del problema, osservando che quella che in origine è una sollecitazione di flessione semplice per la sezione lorda (ad esempio M2+), per la sezione efficace è una flessione deviata, e come tale deve essere trattata.
D'altro canto, pur essendo ΩMy+,eff soggetta a flessione deviata, è sempre possibile definire un numero "W2,eff,+" come il numero che moltiplicato per la tensione di progetto dà il momento limite (che dà luogo a una flessione deviata) sulla sezione efficace. In altre parole, noto il momento limite in flessione deviata sulla sezione efficace (ma con la direzione vettoriale pertinente per la sezione lorda iniziale), dividendolo per la tensione di progetto si ottiene il modulo di resistenza cercato.
6) Il problema del computo dei gr
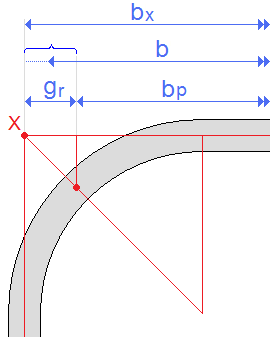
![Definizione di gr (da [1]).](norma_1.zoom70.png)
Definizione di gr (da [1]).
Come già accennato, nel caso di presenza di raccordi curvilinei, questi devono essere rimossi per poter lavorare su lati rettilinei. Questa necessità deriva dal fatto che il comportamento a instabilità locale di un lato rettilineo di lunghezza br con raccordi curvilinei aggiunti agli estremi, non è correttamente valutato impiegando come rapporto tra la larghezza e lo spessore t, il rapporto br/t. In questo modo la lunghezza del lato è sottostimata, a sfavore di sicurezza.
Dunque, non fosse altro che per valutare correttamente la larghezza da impiegare nel calcolo di "b/t", occorre usare un valore intermedio tra la lunghezza netta del tratto rettilineo ("br") e la lunghezza "bx" che si otterrebbe prolungando la linea media dei due lati rettilinei adiacenti, raccordati da un lato curvilineo, sino al punto "X" della figura precedente (si veda anche la figura successiva). Se indichiamo con la norma con "bp" la lunghezza da adoperare per il calcolo dei rapporti larghezza spessore (bp/t), risulta (si veda la figura):
bp=bx-gr
gr= rm [tan(ϕ/2)-sin(ϕ/2)]
essendo rm il raggio medio del raccordo.
Fin qui, è tutto chiaro.
Non è invece del tutto chiaro, nella norma, se la sezione resistente efficace debba includere o meno i tratti gr che si sono scomputati per calcolare bp. Alcuni Autori ([10]) riaggiungono i tratti gr al calcolo delle aree efficaci (pur avendo calcolato le parti non efficaci ed efficaci sulla base della lunghezza bp), altri Autori, tra cui chi scrive (Autore) e ([11]), non lo fanno.
Per decidere cosa sia meglio fare è utile osservare che nel caso in cui la sezione sia interamente reagente, e dunque non vi siano parti non efficaci, si vorrebbe ottenere un'area identica o non troppo dissimile da quella della sezione lorda iniziale (coi lati curvilinei). Ebbene, le misure dei lati (pensati interamente efficaci) rettilinei rimanenti dopo la trasformazione sono le seguenti (1 e 2 per il primo e il secondo estremo del lato):
| • | se si riaggiungono i gr: |
b=bx=br+rm,1tan(ϕ1/2)+rm,2tan(ϕ2/2)
| • | se non si riaggiungono i gr: |
b=bp=bx-gr1-gr2=br+rm1tan(ϕ1/2)+rm2tan(ϕ2/2)-gr1-gr2=br+rm1sin(ϕ1/2)+rm2sin(ϕ2/2)
La lunghezza corretta dovrebbe invece essere
br+rm1ϕ1/2+rm2ϕ2/2
Dato che ϕ/2 è compreso tra sin(ϕ/2) e tan(ϕ/2) si potrebbe dire che le due soluzioni sono equivalenti. In realtà si vede chiaramente che l'errore che si commette è maggiore usando la tangente, ovvero riaggiungendo i gr. Ad esempio per le tre pieghe seguenti:
ϕ/2=22,5° ϕ/2=0,392699rad tan(ϕ/2)=0,4142135 sin(ϕ/2)=0,3826834
ϕ/2=45° ϕ/2=0,7853981rad tan(ϕ/2)=1 sin(ϕ/2)=0,7071067
ϕ/2=67,5° ϕ/2=1,1780972rad tan(ϕ/2)=2,4142136 sin(ϕ/2)=0,9238795
Del resto si può scrivere che l'errore è in un caso
etan=tan(ϕ/2)-ϕ/2=sin(ϕ/2)/cos(ϕ/2)-ϕ/2
e nell'altro
esin=sin(ϕ/2)-ϕ/2
e dato che il coseno è <1, etan > esin.
Sulla base di queste considerazioni appare senz'altro più corretto lavorare scomputando i gr dal calcolo delle parti efficaci. Tuttavia, dato che la autorevole pubblicazione [10] usa un sistema diverso (non si sa se per errore o per convinzione), si è scelto di dare all'utente la possibilità di scegliere tra i due approcci. Così, in CLASS4, se viene sempre usato
bp=b-gr
ai fini del calcolo delle parti efficaci del tratto rettilineo di lunghezza bp, mediante il rapporto bp/t, a queste parti efficaci viene aggiunta una quantità fissa -per ogni estremo "e"- di tratto pieno pari a
(1-Kgr)gr,e
essendo Kgr un fattore compreso tra 0 ed 1.
Il valore proposto dal programma (default) è Kgr=1, ovvero lo scomputo definitivo dei gr dal calcolo delle parti reagenti.
Se si sceglie Kgr=0, allora si simula la procedura usata in [10] che riaggiunge ad ogni estremo "e" un tratto pieno pari a gr,e.
Se si sceglie un valore compreso tra 0 ed 1 si sceglie una via intermedia.
Infine una ultima molto importante osservazione. In funzione della misura del raggio medio rm, può capitare che la eliminazione dei tratti rettilinei (quindi fuori sezione) ottenuta scomputando i gr (Kgr=1), dia luogo ad una sezione fittizia (notional) nella quale i lati sono disgiunti, ovvero presentano dei vuoti tra uno e l'altro. Ciò avviene in particolare per ϕ/2=45° se
gr > t/2
ovvero se
t < 2gr
A nostro parere tale circostanza è attesa e corretta e non inficia minimamente la bontà dell'algortimo. Infatti, abbiamo riscontrato in [11] che di fronte alla presenza di questi vuoti, l' Autore trasla i lati mantenendone inalterata la lunghezza al fine di riempire i vuoti che si creano (per così dire "ricompatta" i lati). Ebbene: tale procedura non è a nostro parere condivisibile perchè mutando l'ingombro della sezione mutano significativamente (in certi casi) i suoi momenti di inerzia e quindi i moduli di resistenza, dando luogo a valori probabilmente a favore di sicurezza, ma troppo penalizzati. Come si vedrà nella validazione, tale circostanza spiega differenze anche piuttosto sensibili riscontrate nel calcolo.
7) Il problema della verifica di stabilità degli irrigidimenti (distorsional buckling)
7.1) Generalità
Il problema dei profili in parete sottile è fondamentalmente costituito dalla possibile contemporanea presenza di ben tre forme di instabilità: la locale, la distorsionale e la globale (di membratura). L'interazione tra le prime forme di instabilità e la terza è trascurata dalla norma, che per la verifica a stabilità della membratura adotta un formato ibrido (si veda quanto detto a critica in [6] a proposito del punto 6.3.1.3.(1) della EN 1993-1-1). Nel lavoro [8]-[9] si è criticato tale approccio mostrando che si perviene ad un quadro molto più chiaro tenendo conto di tale interazione. Sintetizzando, è inutile calcolare i valori efficaci con la tensione di progetto se, a causa della instabilità globale, i valori di tensione di compressione di progetto non si potranno mai raggiungere. Inoltre, la verifica a stabilità dell'asta compressa deve essere fatta usando la stessa identica sezione ΩN-, e non una volta la ΩN- ed una volta la Ω. Tra l'altro si vede che così facendo (ancora in [8] e [9]) si ottengono risultati più precisi.
La EN 1993 esamina invece in dettaglio la interazione tra instabilità distorsionale ed instabilità locale, facendo in buona sostanza ragionamenti vagamente simili a quelli fatti in [8] e [9], ma applicandoli agli effetti della distorsionale sulla locale anzichè anche agli effetti della globale su entrambe. Probabilmente la ragione è consentire di calcolare delle caratteristiche efficaci di sezione che non dipendono dalla lunghezza globale della membratura a cui appartengono.
Con instabilità distorsionale si intende la possibilità che una parte di sezione sbandi come una specie di sotto insieme, distorcendo la forma della sezione. Perchè una parte compressa di sezione si possa instabilizzare da sola, la parte rimanente di sezione deve rimanere al suo posto, e quindi la parte instabilizzata, distorcendo la forma della sezione, trova una certa resistenza. Questa resistenza è eguale lungo lo sviluppo della linea d'asse dell'elemento e dà luogo per la parte instabilizzata ad un carico critico che è quello dell'asta compressa su suolo alla Winkler: l'asta compressa è la sottoparte, il suolo alla Winkler simula il ritegno delle parti che non sbandano. Se As e Is sono l'area ed il momento di inerzia della parte che vuole sbandare da sola, e K è il ritegno offerto dalle parti che non si instabilizzano (e che la trattengono), la tensione critica elastica è pari a (cfr. 5.15 in [1]):
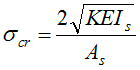
E' da notare che, a differenza di quanto avviene per l'asta di Eulero, la tensione critica distorsionale non dipende dalla lunghezza dell'elemento. Quindi se una parte di sezione voglia instabilizzarsi rispetto ad un'altra è deciso solo dalla geometria della sezione e dal livello di tensione applicata. Se questa però non viene mai raggiunta, perchè si instabilizza prima la membratura, allora il distorsional buckling non si evidenzia sperimentalmente. La tensione che si può applicare, in media, alla parte che si vuole instabilizzare, è data dalla consueta formula (si veda [6] per la dimostrazione della generalità del metodo):
σlim=χfy
χ=χ(λ)
λ=√(fy/σcr)=√(αu/αcr)
La χ=χ(λ) secondo la norma [1], formule (5.12), non segue le normali formule previste per le curve di stabilità a0, a, b, c, d in [12] (EN 1993-1-1):
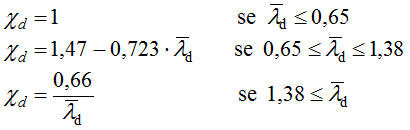
Non è nota a chi scrive la ragione di tale distinzione, che porta a dare χ<1 se λd<0,65 e non come nel caso normale quando λ<0,2. Forse si è introdotta una variazione per meglio compensare altri errori dovuti al metodo proposto, e comunque si è scelto di far intervenire il distorsional buckling solo per snellezze adimensionali (criticità, [6]) già moderatamente alte (>0,65) in modo da toglierselo di torno in molti altri casi.
Se esiste una sottoparte della sezione (che noi qui chiamiamo -per la prima volta a quanto consta- isola) che è soggetta ad una tensione di compressione σ>σlim, allora tale parte non potrà sostenere il livello di tensione applicato e si verificherà la instabilità distorsionale. Il fenomeno viene descritto nella norma per i profili sottili (dove le "isole" prendono il nome di "irrigidimenti di bordo" ed "irrigidimenti intermedi") perchè per questi appare più frequentemente, ma in realtà il ragionamento si può e si dovrebbe applicare a tutti i profili. E' chiaro che al crescere dello spessore dei piatti (t) la rigidezza K cresce (col cubo di t), e quindi σcr tende a diventare molto alta, così che λ tende a essere nulla. Ciò spiega perchè per profili laminati il distorsional buckling non si verifica.
La presenza di possibili "isole" che vogliano sbandare da sole dovrebbe essere sempre indagata e, nel caso in cui si constati che vi deve essere una riduzione di tensione, tale riduzione va applicata. Nel caso dei profili formati a freddo, il metodo previsto dalla norma è involuto e discutibile perchè di fatto funziona in questo modo, riferendoci per brevità ai soli irrigidimenti terminali o "di bordo" (per gli intermedi valgono ragionamenti del tutto simili):
| 1. | Una prima indagine determina le parti non efficaci della sezione che delimitano parti disgiunte di sezione ("isole") il cui comportamento a instabilità va verificato a parte. Le parti terminali disgiunte dal resto che soddisfano certi criteri dimensionali vengono considerate "irrigidimenti di bordo" ("isole" come tutte le altre nella nostra terminologia), e si valuta la loro area As, il loro momento di inerzia Is, ed il ritegno offerto loro dalle altre parti, K, pervenendo a una valutazione della loro σlim. |
| 2. | Se la σlim è inferiore a fy, perchè χ<1 (il che avviene per la norma quando λd> 0,65, (5.5.3.1.(7) in EN 1993-1-3), allora l'"isola", ovvero l'irrigidimento, non può portare la tensione inizialmente ipotizzata potendo portare solo un carico χfyAs e non fyAs. Ne consegue che per ridurre il carico globale agente sulla sezione la norma prevede un trucco, vale a dire, riferendosi al carico afferente sul solo irrigidimento (l'isola), pone: |
(χfy)As=fy(χAs)
ovvero sposta la riduzione dalla tensione fy all'area dell'isola, che viene ad avere uno spessore ridotto χt. In questo modo si potrà far finta che il distorsional buckling non esista e continuare a lavorare su una tensione pari ad fy, ma con un'area per l'isola ridotta a χAs. Se inizialmente si aveva Aeff= A1+As, dopo il trucco si avrà Aeff=A1+χAs.
| 3. | Tale ragionamento della norma, già di per sè molto discutibile e complicato, è ulteriormente complicato dalla opzione che viene data facoltativamente, di raffinare i valori di As e Is sulla base di un nuovo ciclo iterativo. Infatti, a causa del fatto che il livello di tensione sulla isola non è fy ma χfy, le parti efficaci di questa (e solo di questa) saranno in realtà un po' maggiori (a causa dell'effetto σcom già discusso) e dunque l'irrigidimento avrà una area As ed un momento di inerzia Is maggiori. Di tale circostanza (iterazione sull'irrigidimento) CLASS4 tiene opzionalmente conto avendo per default attivato l'opzione. |
7.2) Critiche al metodo di normativa e suoi limiti
Come si è detto il metodo seguito dalla norma è molto discutibile e infatti si devono fare le seguenti critiche:
| 1. | Vi è una sostanziale ambiguità nel fatto che tale ragionamento si applichi al caso degli "irrigidimenti" senza che in realtà esista nè possa esistere alcun criterio fisico e geometrico a priori che possa distinguere ciò che è un "irrigidimento" da ciò che non lo è. Tutte le parti idealmente immaginabili potrebbero sbandare separatamente come "isole", in teoria, ed essere chiamate "irrigidimento" se non lo fanno, e se non lo fanno è solo perchè il loro carico critico è superiore a quello di altre parti (incluso il tutto) che sbandano prima. L'ambiguità sulla definizione della parte di sezione che costituisce l'"irrigidimento" emerge in modo chiaro quando ci si debba occupare di sezioni che non hanno instabilità locale (sono tutte efficaci) ma hanno il distorsional buckling. Non essendoci in questo caso delle discontinuità nella sezione a causa della presenza di parti non efficaci, è quanto meno imbarazzante definire cosa faccia parte dell'"irrigidimento" e cosa no. In [1] il problema non è neppure nominato. In [10] il problema è risolto (esempi alla mano) continuando ad adoperare le stesse formule che attribuiscono una ripartizione tra parte efficace e parte non efficace, ovvero in sostanza prendendo come divisore tra la parte da considerare come "irrigidimento" e la parte che non lo è, il limite a cui tende la parte non efficace di un lato, al tendere a zero della sua estensione (diminuendo b/t sino a che l'estensione della parte non efficace diventa un punto, si annulla). Si tratta di un procedimento non del tutto convincente e non sufficientemente generale, che andrebbe migliorato. CLASS4, comunque, usa questo sistema perchè al momento è l'unico disponibile. In realtà, la separazione tra un isola e l'altra, nel caso di profili interamente reagenti, dovrebbe probabilmente essere trovata lasciando libero il punto di separazione tra un isola e l'altra (mediante una ascissa incognita x), e minimizzando σcr,isola come una opportuna funzione di As(x), Is(x) e K(x). |
| 2. | E' da notare che mentre l'isola che sbanda per χfy continua a lavorare a quel tasso di tensione, χfy, le altre parti lavorano ad una tensione maggiore (e infatti la loro area non è depauperata), il che vuol dire ammettere che raggiunto il primo carico che corrisponde al buckling dell'irrigidimento, successivamente il carico, incrementato, migri verso le parti ancora solidamente in posizione rimanendo costante sulle parti che potrebbero sbandare ("isole saturate", nella nostra terminologia, irrigidimenti al limite, in quella della norma). Tanto varrebbe allora dividere la sezione in parti ("isole") e calcolare il carico massimo su ciascuna disgiuntamente, nonchè quello massimo della isola complessiva per la sua verifica di buckling (come in [8] e [9]) . Infatti nell'algoritmo della norma avviene questo strano gioco di prestigio: un lato che in parte appartiene ad un irrigidimento e in parte no viene calcolato con lo stesso identico ψ, ma con due tensioni di compressione massime diverse: fy per la parte che non appartiene all'irrigidimento e χdfy per la parte che vi appartiene. Insomma, un vero pasticcio. Si noti la figura successiva, presa dalla norma: |
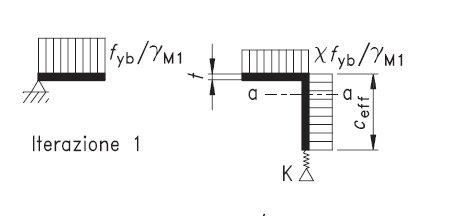
Un lato ha due tratti con tensioni differenti: ciò non è coerente con le ipotesi iniziali (distribuzione lineare di tensione σ)
| 3. | In linea di principio non vi è differenza fisica tra il buckling locale, il buckling distorsionale e quello di membratura, che invece vengono trattati in modo totalmente diverso dalla norma. La ragione per cui si indaga il distorsionale, è che facendo conto che certe parti non si instabilizzino, si fa conto sul fatto che queste siano un ritegno per altre, che sono calcolate di conseguenza (doppiamente appoggiate). Venendo meno il ritegno, viene meno l'ipotesi di partenza. Se ad un lato a sbalzo aggiungiamo una piega minuscola, questa non vale a trasformare il lato a sbalzo in un lato doppiamente appoggiato. Una maggiore unità di approccio sarebbe comunque auspicabile. |
| 4. | L'idea di ridurre lo spessore di una parte di sezione (ed in modo diverso in varie parti) è a parere di chi scrive semplicemente balzana: la forma finale - un po' con certi spessori, un po' con altri- è un ibrido privo di qualsiasi senso fisico ed è tale da indurre in errore chi ne fa uso (la sezione finale, ad esempio, con gli spessori ridotti, non potrebbe sostenere il carico fy(χAeff) se non facendo finta che il fenomeno del distorsional buckling non esista più in natura). |
| 5. | Forse anzichè ostinarsi a lavorare con il formato di verifica delle sezioni lorde anche quando questo non è più applicabile (formato che usa i moduli di resistenza A e W), basterebbe, per rendere tutto più chiaro, scrivere la formula di verifica come |
(N/Nlim)+(My/My,lim)+(Mz/Mz,lim)<1.
L'ambiguità verrebbe meno, non ci sarebbe nessun bisogno di introdurre i chimerici e assurdi spessori ridotti, e tutto sarebbe più chiaro. Si dovrebbe calcolare non Aeff, ma Nlim, e non (i) Weff ma (gli) Mlim.
| 6. | La facoltatività della iterazione sull'irrigidimento è discutibile dato che si trovano valori molto diversi a seconda che questa venga fatta o no (si veda la validazione). |
| 7. | La norma fa solo in modo molto involuto menzione del fatto che un conto è la fy un conto è l'effettivo livello di tensione σcom applicato. Mentre se χd<1 è sempre vero che χdfy<fy, non è detto che χdfy<σcom. Pertanto potrebbe anche capitare che non sia da applicare alcuna riduzione all'irrigidimento (nei problemi flessionali, dove vi è un gradiente di tensione sulla sezione, non è detto che tutti gli irrigidimenti siano compressi a fy). |
| 8. | La norma applica un certo ragionamento alla interazione tra distorsional buckling e local buckling, tenendo conto del livello di tensione del distorsional per calcolare l'entità di diffusione del local, ma omette di fare le medesime considerazioni, come sarebbe logico, per l'interazione tra buckling della membratura e buckling locale (il livello di tensione del global influenza anch'esso il local, cfr [8] e [9]). |
| 9. | Nel suo complesso, la norma appare come la sovrapposizione di ipotesi ad hoc e di trucchi, con varie varianti contemplate e possibili, privi di convincente senso fisico e coerenza, dando luogo ad un aggregato che stenta ad essere compreso ed applicato dalla maggior parte degli aventi diritto. In tali casi, quando i modelli sono complicati e danno luogo a forti errori rispetto ai risultati sperimentali, essi sono semplicemente fatti male. Nondimeno si è nella necessità di usare le norme perchè se no intere tipologie strutturali sono inutilizzabili. |
7.3) Il metodo delle isole, cenni
Per poter affrontare in modo generale il problema occorrerebbe affrontare tutti assieme i tre problemi di buckling locale, distorsionale e globale che sono manifestazioni fisiche dello stesso fenomeno di base: l'instabilità. Ciò si potrebbe fare (ma si danno qui solo accenni) mediante una teoria che introduca sulla sezione un vettore di "isole", funzione del livello di carico applicato, all'interno del quale includere sempre anche la sezione globale (che sia efficace o lorda) come isola globale da verificare.
I valori limite dei carichi da applicare sulla sezione verrebbero trovati ordinando i carichi critici delle varie isole in modo crescente e considerando come limite per la sezione quello che corrisponde alla massima capacità portante.
Il carico della isola globale è limitato dallo sbandamento della membratura nel suo complesso.
Il carico delle isole propriamente dette (isole locali, con instabilità distorsionale) è limitato dal loro carico critico distorsionale corretto dal fattore χd (χdfyAis). Quando un'isola riceve un carico pari al suo limite di compressione è detta saturata.
La capacità portante della membratura (non della sezione che in questo approccio non interessa) è eguale al minimo tra:
| 1. | la somma dei carichi di saturazione di ciascuna isola e |
| 2. | il carico di instabilità della isola globale. |
In certi casi (cfr. [8] e [9] dove il distorsional buckling non era ancora tenuto in conto) se la membratura è sufficientemente snella, la prima isola a sbandare sarebbe proprio quella della sezione globale (spesso coincidente con la lorda), senza che nè distorsional nè (eventualmente) local buckling possano avvenire, e dunque la verifica di resistenza-stabilità unificata porgerebbe
N < Nlim= Nlim, g.
Tale risultato è stato indagato e dimostrato in [8] e [9].
In altri casi, per aste moderatamente tozze, le prime "isole" a sbandare sono proprio delle "isole" propriamente dette, e si ha il distorsional buckling. Ciò avviene quando
ma
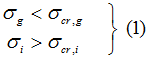
avendo indicato con σg la tensione di compressione media sull'area "isola" globale "g" (efficace o lorda in funzione del livello del carico raggiunto) e con σi la tensione media sull'isola "i".
Anche nel caso di sezione interamente reagente (local buckling assente), occorrerebbe indagare la possibilità che si distacchino isole distorsionali, ricercando le condizioni che diano luogo alle (1). Nel caso di profili formati a freddo con ascissa curvilinea unica si potrebbero cercare in funzione di x i minimi di σcr,i(x), con "i" indice di isola "i".
Il formato di verifica non dovrebbe più prevedere una verifica di stabilità separata da una verifica di resistenza, ma si dovrebbe fare una unica verifica, nella forma già detta (N/Nlim)+.... < 1, come già fatto in [8].
-----------------------------
Copyright © Settembre 2011 Castalia s.r.l.





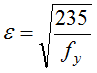
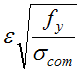
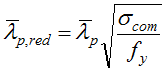

![Definizione di gr (da [1]).](norma_1.zoom70.png)