1. Generalità
2. I file gestiti dalla analisi dinamica non lineare
3. La modellazione dello smorzamento
4. I tipi di integrazione
5. Il passo temporale
6. Impostazioni delle non linearità
7. L'utilizzo delle curve
8. Analisi sismiche singole
9. Analisi sismiche multiple in cascata
10. Analisi dinamiche
11. Tipico risultato di una analisi sismica che termina con il collasso.
12. Tipico risultato di una analisi sismica che termina senza collasso ma con un danno permanente
13. Tipico risultato di una analisi sismica che termina senza collasso e senza un (rilevante) danno permanente.
14. Esempio di analisi dinamica con smorzamento negli elementi
1. Generalità
Le analisi dinamiche non lineari rappresentano lo strumento di elezione per lo studio di molti problemi di ingegneria strutturale, come analisi sismiche, risposta all'impulso (risposta a esplosioni o urti), risposta transitoria a forzanti dinamiche qualsivoglia.
Il solutore che all'interno del pacchetto Sargon fa la analisi dinamica non lineare, si chiama DYNCURAN, ed eredita molte delle funzionalità del solutore NON LINEARE statico CURAN. Il sistema di equazioni che occorre risolvere è
![]()
La matrice delle masse M è formata con gli stessi comandi che si usano per la analisi modale.
La matrice di smorzamento viscoso C viene formata in accordo alle richieste fatte (smorzamento alla Rayleigh, smorzatori concentrati, eccetera).
La matrice di rigidezza tangente Kt segue la evoluzione nel tempo del sistema, considerando a scelta sia la non linearità di materiale che quella geometrica, che quella di contatto.
Infine, la forzante f è un vettore noto, funzione del tempo.
Nel caso delle analisi sismiche con gli accelerogrammi, detto 1r un vettore in cui le componenti valgono 1 per i gradi di libertà traslazionali in r, e 0 tutti gli altri, la precedente equazione diventa
![]()
dove agx(t), agy(t) e agz(t) sono gli accelerogrammi del terreno nelle tre direzioni della struttura, X, Y e Z.
La analisi dinamica non lineare può essere vista come una analisi statica non lineare nella quale ogni stazione, o caso di carico, corrisponde a un passo temporale dT, e sia attivo il load path. In altre parole, ogni caso successivo parte dalla fine del caso (stazione) precedente. Per sua natura, il problema si presenta complicato dal fatto che nelle equazioni compaiono le accelerazioni nodali e le velocità nodali, le quali vengono espresse in funzione degli spostamenti nodali e del passo temporale dT, per mezzo di opportune relazioni di integrazione nel tempo. Dato che una analisi dinamica può durare decine di secondi, e che i passi temporali devono essere sufficientemente piccoli, è facile che una Time History Non Lineare (THNL) possa avere 500-1000 o più stazioni (casi di carico).
Dato che in campo non lineare non vale il principio di sovrapposizione degli effetti, l'analisi deve sempre cominciare con una configurazione di carichi applicati staticamente, che producono nella struttura il campo di spostamenti, sforzi e deformazioni dai quali si parte per la analisi non lineare. Il modo più comodo per fare ciò, e partire da una struttura che abbia un solo caso di carico (statico) il quale corrisponde alla situazione dei carichi al momento in cui parte la analisi. Tipicamente, nel caso sismico, un caso di carico (generato con il comando edit casi combina) che includa i carichi permanenti e i variabili dodati al pertinente (sismico) livello quasi-permanente. Se anziché un caso di carico statico ne è presente più d'uno, il solutore li applica uno dopo l'altro come stazioni con load path, e quindi applica il 2 al termine del 1, e il 3 al termine del 2, sempre partendo dalla configurazione relativa al caso precedente (sforzi, deformazioni, spostamenti).
DYNCURAN farà sì che alla fine della analisi, se NS è il numero di casi di carico statici, e NSTEP è il numero di step dinamici, ci siano NS+NSTEP casi di carico, e NS+NSTEP combinazioni, ognuna delle quali relativa a uno step di carico.
Nel corso della analisi dinamica, essendo i passi temporali piccoli, il programma cerca sempre di convergere applicando lo step dT nella sua interezza. Se non ci riesce, allora lo suddivide in frazioni più piccole, con gli stessi criteri validi per il solutore non lineare statico. Il parametro di carico "lambda", per una certa stazione, ovvero un certo step di carico, corrisponde a 0 all'inizio della stazione e 1 quando dT è stato completamente applicato. Un valore dlambda = 0.2, impica che si si stia muovendo nel tempo di una quantità pari a 0.2dT.
Le analisi dinamiche non lineari sono sensibili alle leggi costitutive dei materiali, e in particolare alla deformazione ultima. Si noti che anche un materiale dichiarato elastico lineare ha una sua deformazione ultima. Il raggiungimento, in una fibra o in un layer (per gli elementi piastra e membrana), di deformazioni equivalenti pari a quella ultima implica la rottura e quindi la inattivazione da quel momento in poi della fibra/layer. Tale inattivazione è irreversibile. Si noti che di fatto il verificarsi di una tale circostanza è un prodromo diretto del collasso, o per lo meno di uno stato di grandissima sofferenza della struttura. Il valore della deformazione ultima da impostare nella legge costitutiva dipende dal materiale, dalla normativa che si sta usando, o dalle specifiche esigenze dell'analista.
Sono possibili tre diversi tipi di analisi dinamica, che saranno spiegati nelle sezioni successive:
•Analisi sismica singola
•Analisi sismiche multiple
•Analisi dinamiche (singole)
In tutti i casi al termine della analisi ci si trova con centinaia di nuovi casi di carico, e di combinazioni, ognuna delle quali corrispondente a un certo istante di tempo t. E' facile capire che la gestione di tutti questi "casi di carico" pone considerevoli problemi, per cui non è di fatto possibile scorrere tali casi dal primo all'ultimo. Occorre un approccio totalmente diverso. Tale approccio fa uso delle "curve", vale a dire di file (esterni al modello) con estensione PMC e che possono essere letti da Sargon con il comando Post-Curve , nei quali sono memorizzate delle curve y=f(x) che hanno un particolare significato fisico e strutturale. Nel caso delle analisi THNL, tali curve sono:
•Curve in cui x è il tempo, e y è una azione interna di un elemento, una deformazione, uno spostamento (velocità o accelerazione) nodale, un interstorey drift, l'energia plastica accumulata nella struttura, la massima deformazione nel modello eccetera.
•Curve in cui x è una deformazione e y uno sforzo (per i cicli di isteresi).
•Curve in cui x è un numero di analisi (nel caso multi sismico) e y è un indicatore della salute della struttura come il volume plastico o l'interstorey drift, al variare della analisi.
Se le curve vengono appropriatamente richieste (si veda la sezione dedicata) prima della analisi esse possono fare la differenza tra un incomprensibile oceano di numeri, e una serie di sensati e utili risulati. Esse, tra l'altro, possono guidare verso gli step di carico più significativi: posizionatisi in quel caso di carico (step), sarà possibile avere tutte le informazioni come spostamenti, azioni interne, stato delle fibre eccetera.
La esecuzione di una THNL avviene preparando il modello preventivamente, e quindi essenzialmente (si consiglia):
•Nel caso delle analisi sismiche tenendo un solo caso di carico statico (carichi permanenti e quasi permanenti) e nessuna combinazione. In alternativa pochi casi che saranno applicati in serie uno dopo l'altro. E nessuna combinazione.
•Nel caso delle analisi dinamiche, tenendo solo un caso di carico statico e tanti casi dinamici quanti sono strettamente necessari, e nessuna combinazione. In alternativa pochi casi statici anziché uno.
A valle di una THNL è possibile rieseguirla, senza bisogno di cancellare i casi di carico e le combinazioni generati automaticamente dalla precedente analisi. Ciò viene fatto automaticamente.
Attenzione a non chiedere THNL su modelli con combinazioni che ha interesse NON perdere. Di norma, le analisi THNL vengono fatte su una copia del modello originario. In ogni caso, il programma avvisa prima di procedere.
Si esegue poi il comando File-Analizza, scegliendo Time History Non Lineare. Ciò porta al dialogo Time History Non Lineare.
2. I file gestiti dalla analisi dinamica non lineare
Viene creato un file .CUI del tutto identico al file di input per CURAN.
Viene poi creato un file .DNL di input specifico per DYNCURAN.
Nel corso della analisi vengono creati (in aggiunta ai file normali) i file:
. VDB con le velocità nodali (binario)
.ADB con le accelerazioni nodali (binario)
.YOG file di log della analisi (ASCII)
.YOU file di output della analisi (ASCII).
3. La modellazione dello smorzamento
In questa sezione ci si riferisce allo smorzamento viscoso "inerente" e alla presenza di smorzatori viscosi concentrati, i quali entrambi concorrono alla matrice di smorzamento viscoso C. Si noti che anche la plasticizzazione comporta dissipazione di energia e perciò smorzamento, ma tale "smorzamento plastico" non è governato dalla matrice C bensì dai cicli di isteresi presenti nelle fibre.
Per quanto riguarda lo smorzamento viscoso inerente (ovvero proprio della struttura, non relativo a specifici dispositivi), questo è gestito al momento mediante la modellazione alla Rayleigh, la quale consente di specificare due valori di smorzamento relativo al critico relativi a due periodi diversi. La modellazione alla Rayleigh viene usata per compatibilità con le analisi THM, nelle quali è sostanzialmente usata perché consente il disaccoppiamento dei modi.
Per quanto riguarda gli smorzatori viscosi concentrati (per esempio legati alla interazione suolo-struttura, o relativi a specifici dispositivi accoppiati, ad esempio, ai diagonali di controvento), essi sono gestiti da DYCURAN, e sono previsti da Sargon dove è possibile associare uno smorzamento sia agli elementi biella che alle molle. Per un esempio di utilizzo degli smorzatori concentrati si veda la prossima sezione 14 . La assegnazione degli smorzamenti agli elementi molla si fa quando vengono aggiunti. La assegnazione dello smorzamento associato a un elemento biella si fa con il comando Gap e Attrito
4. I tipi di integrazione
Per risovere il sistema di equazioni differenziali è necessario integrare le equazioni del moto nel tempo. Sono possibili vari metodi, DYNCURAN implementa il metodo di Newmark e il metodo Wilson-θ.
Il metodo di Newmark dipende da due parametri detti β e γ. Il metodo di Wilson, dipende dal valore di un parametro detto θ.
Nel metodo di Newmark, le accelerazioni e le velocità al passo (n+1) vengono fatte dipendere dalle accelerazioni e velocità al passo precedente, n, e dall'incremento incognito dello spostamento da n a n+1 (Δu):

A meno che non ci siano buone ragioni, si consiglia di usare il metodo di Newmark con i valori già impostati. Esso risulta migliore e più stabile del metodo di Wilson, che pure è stabile, ma tende a smorzare i modi con periodo breve.
L'argomento è specialistico e non è possibile in questa guida trattarlo approfonditamente. Per avere maggiori ragguagli si rimanda ai testi:
Crisfield M. A., Non-linear Finite Element Analysis of Solids and Structures, Volume 2: Advanced Topics, John Wiley & Sons, 1997
Bathe K. J., Finite Element Procedures, Prentice Hall, 1996
Chopra A., Dynamics of Structures, Prentice Hall, 2001
Clough R. W., Penzien J., Dynamics of Structures, McGraw-Hill, 1982
5. Il passo temporale
La scelta del passo temporale (dT, o meglio sarebbe scrivere Δt) , ha importanza perchè influisce da una parte sulla precisione della analisi, dall'altra sulla mole di dati di output e sulla durata della analisi in termini computazionali.
Considerando la decomposizione modale della struttura, si raccomanda che il dT non sia più grande di 1/10 del periodo dei modi che si considerano importanti per la struttura. Dato che spesso i modi dominanti sono intorno a 0.8-1.5 secondi, il dT non dovrebbe mai essere più grande di 0.08-0.15 sec.
Il valore correntemente usato, che rappresenta un buon compromesso tra le esigenze opposte è 0.05, ovvero 5 centesimi di secondo. Ciò implica 200 passi ogni 10sec di analisi. In certi casi, può essere opportuno però usare un passo minore. Se ad esempio si studia un impulso della durata di 1/100 di secondo, non ha molto senso usare un passo 5 volte più grande. Con passi molto piccoli, può avere senso ridurre la durata della analisi. Nel caso delle analisi sismiche, tenendo presente che la durata di un segnale è di solito intorno ai 30 secondi (600 passi con dT=0.05), ma può anche facilmente arrivare ai 50, il valore 0.05 sembra mediamente appropriato. Spesso la campionatura degli accelerogrammi ha passo sensibilmente inferiore, come 1/100 sec, o 5/1000. Ciò è positivo in quanto fare una analisi con un dT pari o inferiore alla campionatura della forzante, porta a considerevoli errori.
Ovviamente, casi particolari richiedono valori diversi. Strutture che abbiano periodi più lunghi e per le quali la durata debba protrarsi per molte decine di secondi, o strutture con periodi brevi che siano solleciate impulsivamente per periodi di tempo brevissimi. Il valore 5/100 deve essere considerato puramente indicativo.
Lo studio della sensitività dei risultati della analisi al passo temporale dT, può aiutare a confermare la bontà della scelta fatta. Invece, in presenza di variazioni significative (magari esplorate nei primi secondi della analisi), il passo dovrà essere ridotto. Anche in presenza di forti escursioni plastiche e di sofferta convergenza, la riduzione del passo temporale può molto aiutare. Se si vede che nel corso di una analisi la parte difficile da sostenere per la struttura è tra 12 e 16 secondi, si può ad esempio ripetere la analisi con una durata di solo 20 secondi ma passo dimezzato.
6. Impostazioni delle non linearità
La impostazione del calcolo non lineare si fa con lo stesso identico dialogo che usa anche il solutore CURAN. Valgono quindi tutte le osservazioni fatte nella sezione Come fare Analisi non lineari con il solutore CURAN, con alcune specificità ed eccezioni, che sono le seguenti.
•Nelle analisi non lineari dinamiche è sempre per definizione attivata la opzione "load path", indipendentemente da cosa si scelga.
•Ogni stazione rappresenta un istante diverso, che differisce dal precedente e dal successivo per dT. Non ha quindi molto senso dividere la stazione in step eguali come si fa per i casi di carico statici. Il solutore dinamico DYNCURAN utilizza quindi sempre un passo iniziale pari all'intero dT e lo riduce automaticamente in funzione della difficoltà a convergere (diminuzione automatica ampiezza passo). Ha quindi importanza il "desiderato numero di iterazioni" per la scelta automatica della drasticità della riduzione/aumento, dello step di carico dλ all'interno del passo temporale dT. Inizialmente dλ= 1, e quindi dT. Se non si riesce a convergere (sulla base delle tolleranze indicate) allora si usa dλ minore di 1, e dλdT.
•Nel corso della analisi viene indicato sempre l'istante corispondente alla stazione esaminata. Tutte le analisi partono da un tempo (convenzionale) negativo per accomodare la parte statica, l'istante 0 corrisponde alla fine della parte statica. Poi gli istanti saranno dT, 2dT, 3dT, e così via.
7. L'utilizzo delle curve
Come detto l'utilizzo delle curve aiuta enormemente nella interpretazione dei risultati di una THNL.
Ci sono due insiemi di curve: quelle che sono aggiunte sempre e quelle che si riferiscono ai nodi e agli elementi (trave e biella) selezionati nel serbatoio 3 all'atto della esecuzione della analisi.
Sono sempre aggiunte:
1.La curva che dà il volume elastico di travi e bielle in funzione del tempo. Se tale volume non varia la struttura resta in campo elastico (nelle bielle e travi).
2.La curva che dà il volume plastico di travi e bielle in funzione del tempo. Per "volume plastico" si intende il volume di materiale in travi e bielle che, in un certo istante, è nella situazione "loading" ovvero sul luogo plastico. Tale volume può diminuire se il materiale rientra in campo elastico con uno scarico (unloading).
3.La curva che dà la il volume di materiale dichiarato "rotto" in funzione del tempo.
4.La curva che dà la percentuale di volume plastico sul totale in funzione del tempo.
5.L'indicatore dello stato di salute della struttura "HEALTH EPS" in funzione del tempo. Si tratta della massima deformazione negli elementi trave e biella, in un certo istante. Si considera il massimo al variare degli elementi.
6.L'indicatore dello stato di salute della struttura "HEALTH IDR" in funzione del tempo. Si tratta del massimo interstorey drift letto nella struttura, istante per istante. L'IDRIFT dipende dai nodi selezionati nel serbatoio 3: tipicamente si selezionano tutti i nodi di un certo allineamento verticale. Il programma tiene sotto controllo le coppie di nodi posti al piano successivo. L'IDRIFT è inteso come composizione vettoriale dei DRIFT in direzione X e Y, ovvero è la radice quadrata della somma dei due quadrati, drift X2 e drift Y2. Se ade esempio sono selezionati 8 nodi, ci saranno 7 coppie di nodi monitorati, e, il massimo IDRIFT tra i sette, in ogni istante verrà plottato. E' naturalmente possibile selezionare anche più allineamenti.
Per ogni nodo selezionato nel serbatoio 3 sono aggiunte le seguenti curve:
1.Traslazione X, Y, Z in funzione del tempo.
2.Rotazione X, Y, Z in funzione del tempo.
3.Velocità traslazionali e rotazionali X, Y, Z in funzione del tempo.
4.Accelerazioni traslazionali e rotazionali X, Y, e Z in funzione del tempo.
Per ogni biella selezionata nel serbatoio 3 sono aggiunte le seguenti curve:
1.Percentuale di volume plastico e percentuale di volume rotto in funzione del tempo.
2.Azione assiale in funzione del tempo.
3.Deformazione in funzione del tempo
4.Sforzo in funzione della deformazione.
Per ogni trave selezionata nel serbatoio 3, sono aggiunte le seguenti curve:
1.Massima deformazione al variare di tutte le fibre componenti, in funzione del tempo.
2.Percentuale di volume plastico in funzione del tempo.
3.Percentuale di volume rotto in funzione del tempo.
4.Rotazione del primo estremo e del secondo estremo in funzione del tempo.
5.N, T2, T3, M1, M2, M3 al primo estremo in funzione del tempo.
6.N, T2, T3, M1, M2, M3 al secondo estremo in funzione del tempo.
Le curve sono salvate in un file con estensione PMC al termine della THNL, e sono leggibili con il comando Post-Curve.
8. Analisi sismiche singole
Un primo modo di usare il solutore dinamico non lineare è eseguire analisi sismiche singole. Per fare queste analisi occorre scegliere da 1 a 3 accelerogrammi (dialogo Time History Non Lineare) tra quelli memorizzati nella struttura per mezzo del comando di importazione Edit-Azioni-Accelerogrammi.
•Se si sceglie un solo accelerogramma questo sarà applicato in una sola direzione scelta dall'analista (o X, o Y, o Z).
•Se si scelgono due accelerogrammi, questi devono essere ondulatori (non marcati Z, sussultori) secondo due direzioni ortogonali tra loro. Devono inoltre appartenere al medesimo evento (naturale o simulato). In questo caso è solo possibile specificare come direzioni di applicazione alla struttura la X e la Y. I segnali saranno trasformati vettorialmente alle direzioni della struttura X e Y, noto che sia l'angolo formato dall'asse X della struttura con l'angolo dell'asse geografico WE. Ad esempio, la direzione Nord è +90°, la direzione Sud è +270° (l'angolo è positivo se antiorario).
•Se si scelgono tre accelerogrammi, una tripletta, di questi segnali, tutti riferiti al medesimo evento, uno deve avere direzione verticale, Z, gli altri due devono rispettare le stesse condizioni del punto precedente, e sono allo stesso modo convertiti alle pertinenti direzioni X e Y della struttura.
Va infatti osservato che quando vengono letti e importati gli accelerogrammi, questi hanno una certa direzione, definita, appunto, rispetto all'asse geografico WE. Specificare l'angolo dell'asse X della struttura ha sempre importanza, ma naturalmente ne ha una particolare quando si facciano analisi sismiche simulando diversi scenari sismici. In questo caso, la congiungente il sito con la faglia (ammesso un meccanismo di rottura puntuale), detta direzione radiale, o Strike, ha una direzione diversa da scenario a scenario, da faglia a faglia. E' stato dimostrato mediante un corposo insieme di analisi numeriche, che la orientaizone mutua dell'edificio e dei segnali è fondamentale al fine di cogliere appropriatamente gli effetti sismici.
Per approfondimenti si veda:
Come saperne di più del metodo neodeterminitico
Come affrontare le analisi sismiche coi segnali
Come utilizzare EDEM (Elastic Deformation Energy Maximization)
Come gestire l'inviluppo dei segnali
9. Analisi sismiche multiple in cascata
In questo caso il programma lancia DYNCURAN molte volte una dopo l'altra, allo scopo di eseguire due o più analisi sismiche dinamiche non lineari (tipicamente alcune decine, ma il programma è stato usato per lanciare sino a 400 analisi sismiche in cascata).
Quante analisi, e con quali segnali, è determinato da quanti e quali segnali sono stati selezionati mediante il comando Edit-Azioni-EDEM, prima della analisi.
Come nel caso precedente, è possibile usare segnali singoli (un segnale = una analisi), applicati in una delle tre direzioni; coppie di segnali (due segnali relativi allo stesso evento, in direzioni tra loro ortogonali e selezionati = una analisi); o triplette di segnali (tre segnali relativi allo stesso evento, uno in direzione Z, due in direzioni ortogonali tra loro, tutti e tre selezionati = una analisi). Ad esempio se si sono selezionati 300 segnali a triplette, e si usa X, Y e Z, saranno esaminati 100 eventi diversi.
Il programma alla fine lascerà il modello nello stato congruente con la ultima analisi (casi e combinazioni).
Tuttavia, e questo è molto importante, avrà anche creato un file con delle speciali curve, che, analisi per analisi, monitorano gli indici di salute della struttura, in modo da avere poi una idea di quali simulazioni (eventi) siano le peggiori per la struttura in esame. Le curve sono dunque curve del tipo Health = Health(event) e consentono di comprendere quali siano le THNL più indicative per la struttura in esame. Per i dettagli su come sia chiamato il file con le curve, e su cosa contengano le curve, si veda il dialogo Time History Non Lineare.
Inoltre, per ogni analisi eseguita, viene creato e salvato il file .PMC con tutte le curve tipiche della singola analisi sismica: questo consente di tracciare quanto è avvenuto in ogni analisi con grande dettaglio, senza il bisogno di memorizzare tutti gli step delle N analisi lanciate (che porterebbe ad avere troppi casi salvati nel modello, ad esempio 50 analisi con 800 passi comporterebbero 40 mila casi).
Se tali analisi vengono lanciate dopo aver ordinato i segnali, le coppie di segnali, o le triplette di segnali, in ordine di energia elastica di deformazione incassata massima mmediante il comando EDEM, di regola si vede con sufficiente ma non assoluta regolarità che gli eventi analizzati per primi sono i più severi, mentre quelli analizzati per ultimi sono i meno severi.
Attenzione: in funzione della dimensione del modello, la MULTI analisi sismica può implicare tempi di calcolo lunghi o lunghissimi.
10. Analisi dinamiche
Per analisi dinamiche si intendono analisi nelle quali alla struttura siano applicate forze funzione del tempo. In Sargon queste forze devono essere descritte mediante uno o più casi di carico che ricevano la etichetta "DINAMICO", e a essi viene associata una certa funzione del tempo t. (si veda il comando Edit-Azioni-Casi-Aggiungi e il dialogo Funzione del Tempo).
Tutti i casi dinamici sono applicati contemporaneamente, a partire dall'istante t=0. Se ad esempio al caso L3 è associata la funzione f(t) e al caso L4 la funzione g(t), la analisi dinamica andrà ad applicare L3f(t) + L4g(t).
Sono tipici problemi che richiedono analisi dinamiche:
•Risposta all'impulso (urti, esplosioni)
•Risposta al gradino (improvvisa applicazione di forze che restano poi costanti)
•Forzante armonica causata da masse rotanti eccentriche (macchine in quota o su fondazioni)
•Transitori di avvio o spegnimento di macchine
•Raffiche di vento
•eccetera
Si tenga presente, nel definire le f(t) che la THNL comincia sempre invariabilmente al tempo t=0.
11. Tipico risultato di una analisi sismica che termina con il collasso.
Si mostrano alcune immagini relative a una analisi che non è terminata a causa del collasso della struttura, causato dalla rottura improvvisa di qualche elemento strutturale fondamentale.
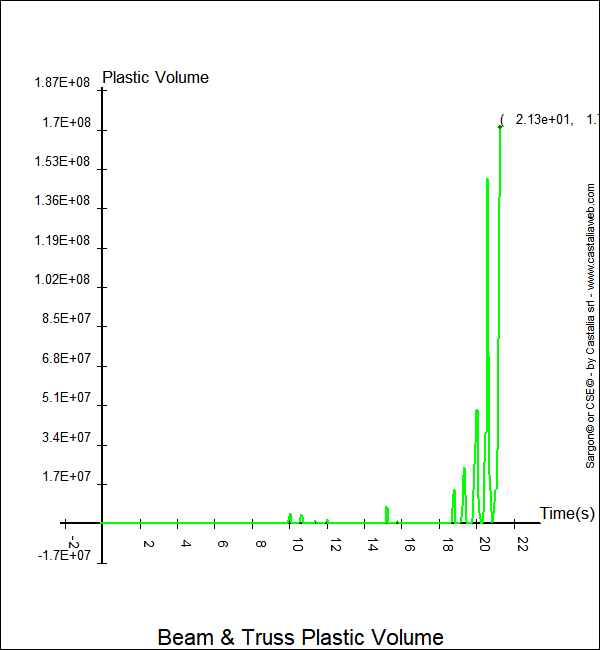
Figura 1. Volume plastico in funzione del tempo
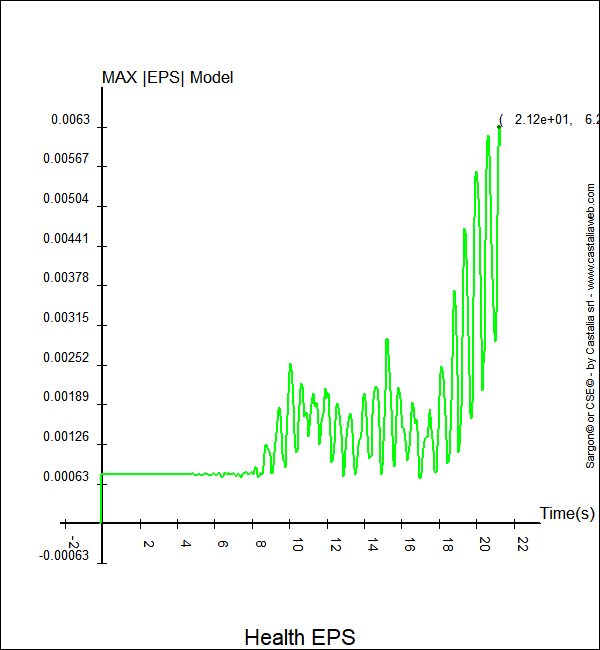
Figura 2. Massima deformazione nelle fibre del modello al variare del tempo

Figura 3. Massimo interstorey drift nel modello al variare del tempo
Nelle tre figure si vede che la analisi non è arrivata a termine. Il volume plastico è in fase di rapido accrescimento, e così la massima deformazione e l'interstorey drift. L'analisi si interrompe bruscamente, perché lo step successivo implica la rottura di fibre e la impossibilità di convergere sul residuo nullo.
12. Tipico risultato di una analisi sismica che termina senza collasso ma con un danno permanente
Si mostrano alcune immagini relative a una analisi che è terminata senza il collasso della struttura, ma lasciandola permanentemente e significativamente danneggiata.
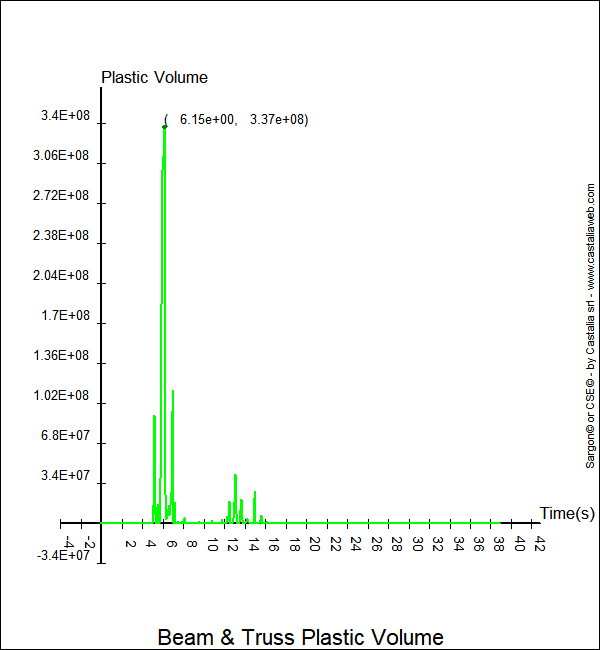
Figura 4. Volume plastico in funzione del tempo
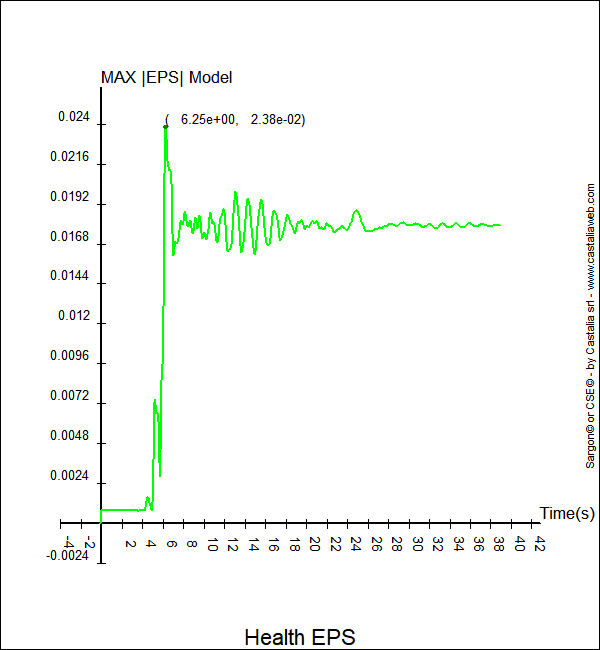
Figura 5. Massima deformazione nelle fibre in funzione del tempo
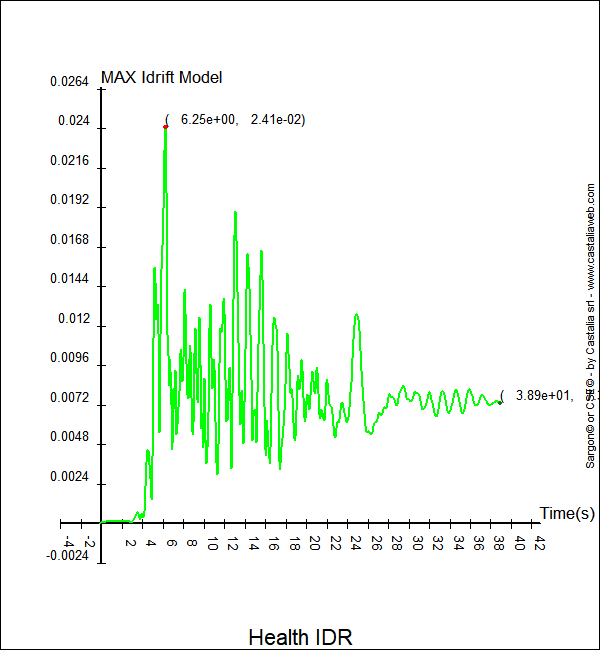
Figura 6. Massimo interstorey drift al variare del tempo
In questo caso, la analisi è arrivata a termine, dpo aver passato delle fasi di plasticità significativa e di lenta convergenza.
In particolare, Figura 4, il massimo volume che in un certo istante è stato nella condizione "loading" (ovvero sul luogo plastico), in tutti gli elementi, è pari a 3.37e8 mm3, vale a dire 0.33 metri cubi. Ciò avviene a 6.15 secondi dall'inizio della analisi. Si noti come ci siano altri picchi, ma meno pronunciati, e come poi al termine della analisi il volume plastico sia nullo. Ciò non vuole dire, come vedremo, che non ci siano deformazioni plastiche permanenti, ma solo che tutte le fibre sono rientrate in campo elastico e non si trovano sul dominio limite, in una condizione che tecnicamente è detta "loading".
Interessantissime, per il loro valore di "firma" di danno permanente, sono le due curve successive.
Nella prima, Figura 5, si vede la massima deformazione (totale) nelle fibre del modello. Qui, il picco, prossimo ma non oltre la deformazione ultima impostata in questo modello (2.53%), è a 6.25 secondi, ovvero 1/10 di secondo dopo il momento in cui era massimo il volume plastico, e vale 0.0238, 2.38%. Nello scorrere il campo plastico, qualcosa è andato in "unloading" ritornando alla fase elastica cosicchè il picco di volume è diminuito significativamente (2.45e7 mm3 a t=6.25 sec). In questo esempio il materiale era elastico perfettamente plastico. Al termine della analisi, al secondo 38.9, nel modello resta una deformazione pari a 1.78%, ben al di là, circa 10 volte di più, della deformazione allo snervamento pari a εy=355/210000= 1.69 e-3 = 0.169%.
Nella Figura 6, si vede bene l'andamento del massimo Interstorey Drift al variare del tempo, e, soprattutto, si vede che al termine della analisi resta un danno permanente, ovvero la struttura non è più dritta ma ha una deformazione permanente alla quale è associato un massimo interstorey drift pari a 7.3e-3. Ciò vuol dire che su 4m di interpiano si avrebbe uno spostamento permanente di 29.2mm, circa 3cm. Si noti anche come il massimo Interstorey Drift avvenga proprio quando è massima la deformazione, all'istante 6.25. In quell'istante l'IDRIFT valeva 2.41e-2, che, su un interpiano di 4m, corrisponde a uno spostamento di 96.4 mm, quasi 10cm.
13. Tipico risultato di una analisi sismica che termina senza collasso e senza un (rilevante) danno permanente.
Si mostrano alcune immagini relative a una analisi che è terminata senza il collasso della struttura, e senza danni significativi.
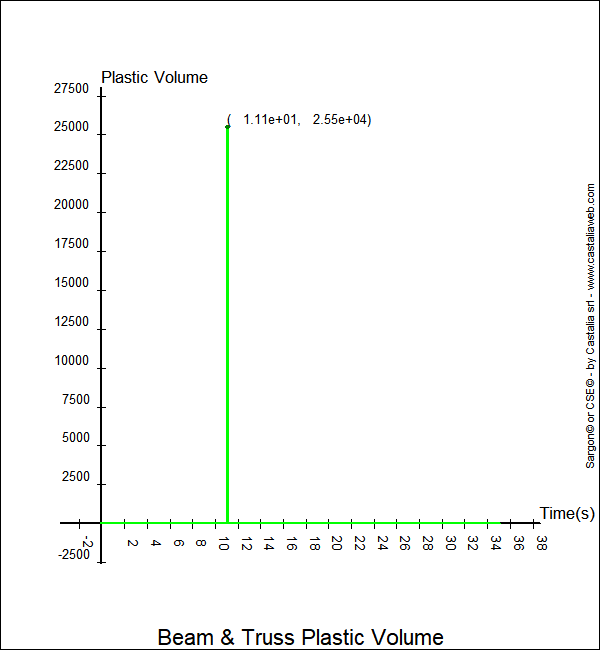
Figura 7. Volume plastico in funzione del tempo
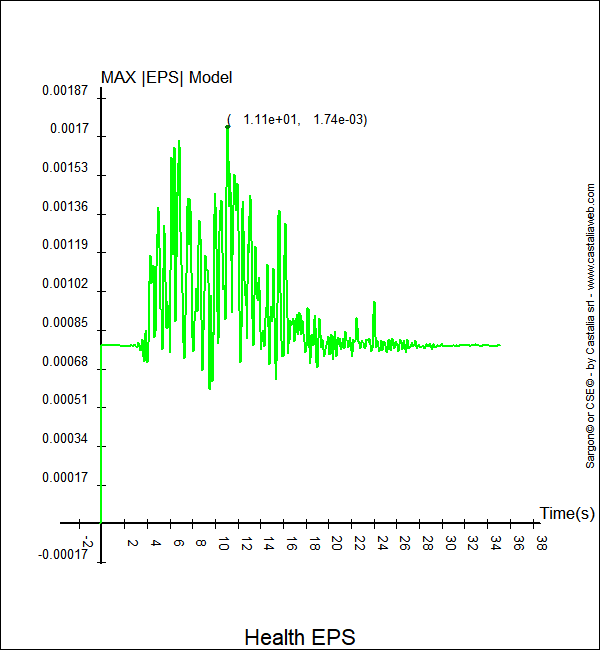
Figura 8. Massima deformazione nelle fibre in funzione del tempo
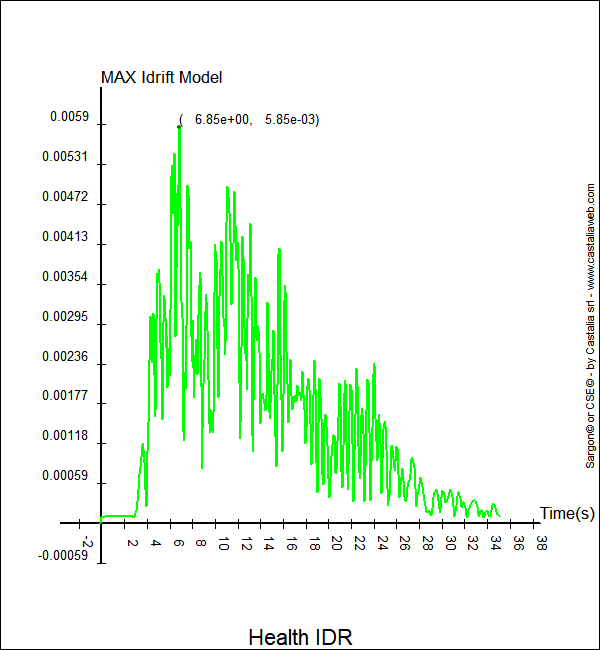
Figura 9. Massimo interstorey drift al variare del tempo
Anche in questo caso, la analisi è arrivata a termine.
Nella Figura 7, si vede che il volume plastico si mantiene sempre nullo, ad eccezione di un breve istante in cui raggiunge un valore puntuale di 2.55e4 mm3, vale a dire 25.5cm3. Si tratta quindi di un fatto sostanzialmente insignificante per la struttura.
Nella Figura 8, si vede come la massima deformazione nel modello sia pari a 1.74e-3, che corrisponde a una tensione elastica pari a 365.4 > fy. In effetti questa deformazione è al di là dello snervamento, e rappresenta una modesta plasticizzazione (la tensione è in realtà 355 MPa). L'istante corriponde a quello di massimo volume plastico. Si noti che al termine della analisi la massima deformazione torna al valore iniziale, che è 7.81e-4, al quale corrisponde una tensione massima pari a 164MPa.
Analogamente, nella Figura 9, si vede che il massimo Interstorey Drift torna al valore iniziale, che è un valore molto basso e compatibile con carichi orizzontali praticamente nulli. Questo vuole dire che la struttura è sostanzialmente rimasta in campo elastico e che non ha subito danni permanenti dall'evento simulato (con una tripletta di accelerogrammi).
14. Esempio di analisi dinamica con smorzamento negli elementi
In questa sezione si fa vedere un esempio di analsi dinamica, con molti elementi (molla) ai quali è stato dato, oltre a una rigidezza, anche uno smorzamento viscoso. Il problema è studiato per essere a molti gradi di libertà ma al tempo stesso assimilabile a un problema di oscillatore semplice soggetto a oscillazioni forzate, con smorzamento viscoso.
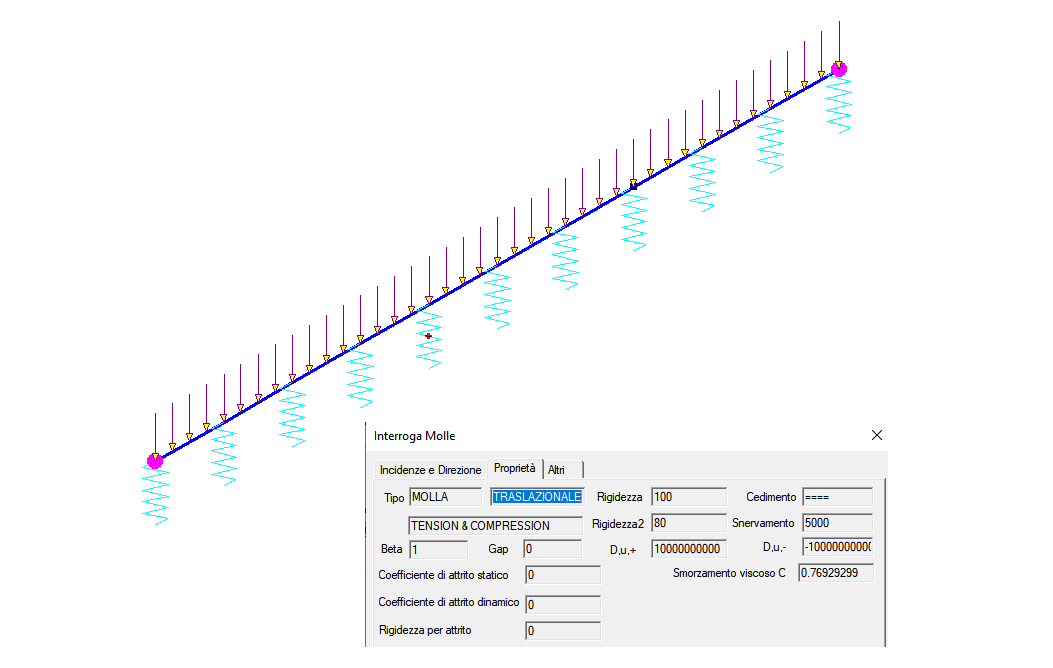
Data una asta divisa in 10 parti, essa abbia un peso di 3628.56N, corrispondente a una massa di 369.8837 Kg. L'asta è adagiata su un letto di molle relativamente cedevoli, aventi una rigidezza complessiva di 1.000.000 N/m=1.000N/mm. La oscillazione propria del sistema si ottiene come

Nel primo caso di carico mettiamo solo il peso proprio. Nel secondo caso di carico, etichettato "DINAMICO" mettiamo 10.000N in mezzeria.
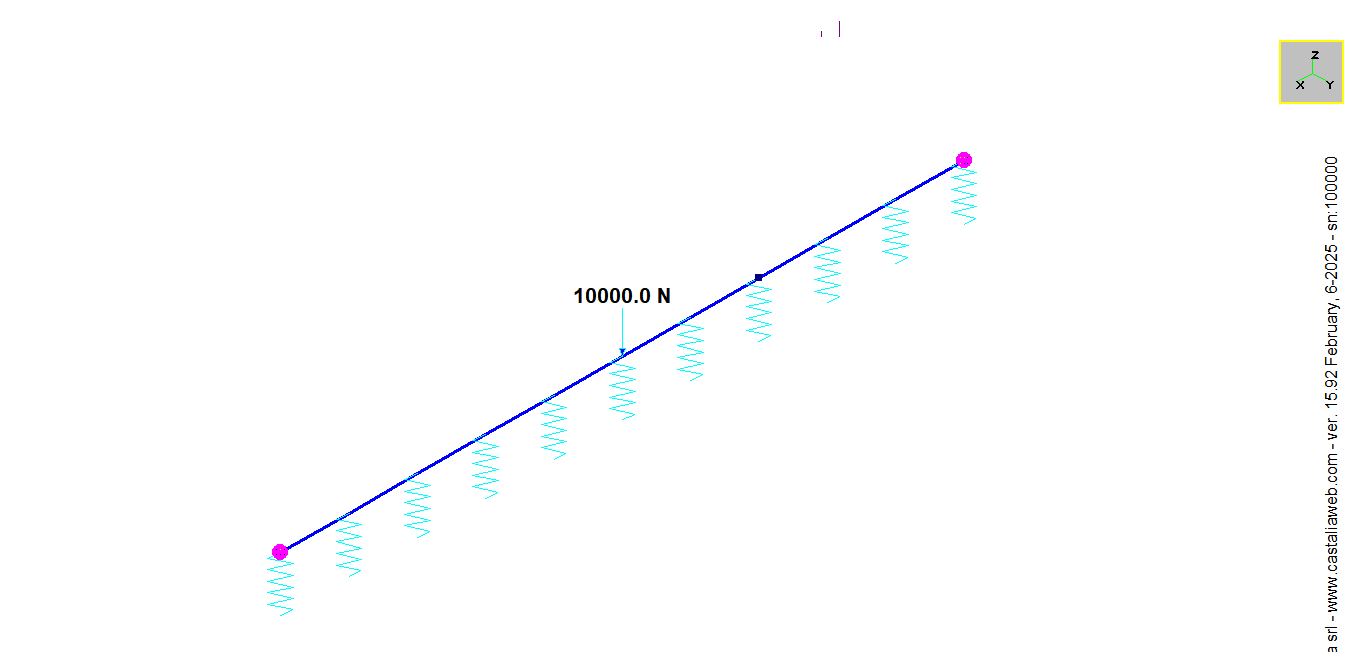
Associamo a questa forza F una funzione sinusoidale del tempo f(t) avente lo stesso periodo proprio della struttura, e quindi in risonanza (sarà dunque applicata F f(t) ):
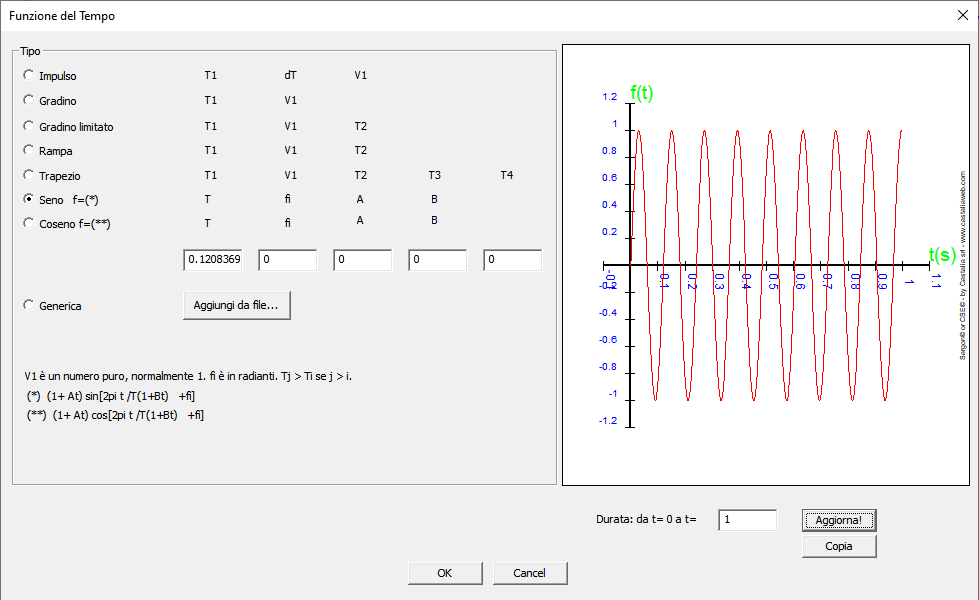
La forza messa al centro e il letto di molle cedevole implicano un atto di moto periodico puramente traslatorio verso il basso. Scegliamo di applicare uno smorzamento relativo al critico del 20%, il che implica uno smorzamento C pari a:
![]()
Nota la rigidezza complessiva e lo smorzamento complessivo dell'oscillatore, si può calcolare la rigidezza delle molle interne dividendo per 10, e quella delle molle esterne dividendo per 20. Analogamente per lo smorzamento. Se si lavora in N, mm, sec, si ottiene

Applicando tali valori di rigidezza e smorzamento alle singole molle, si ottiene una rigidezza K e uno smorzamento C pari a quelli complessivi (si veda la interrogazione dell'elemento biella).
Come è noto dalla teoria, la risposta a una oscillazione forzata armonica in risonanza con la frequenza propria, amplifica la risposta statica per un fattore Q pari a
![]()
Nel nostro caso la risposta statica è data da F/K= 10.000/1000 = 10 mm. Ne consegue che dovremmo trovare oscillazioni forzate, passato il transitorio, con ampiezza 25 mm. Il periodo di tali oscillazioni forzate coincide con il periodo della forzante.
Eseguita la analisi dinamica non lineare, avendo però impostato un comportamento lineare, con dT=0.001 sec e ΔT=1sec, si ottiene per lo spostamento nel nodo iniziale la seguente curva funzione del tempo:
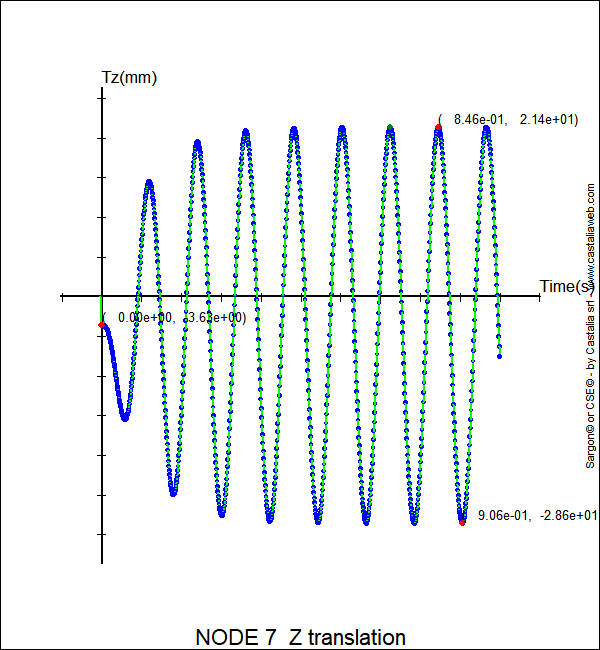
Si vede che:
•Dopo un periodo transitorio, le ampiezze si stabilizzano e la differenza tra massimo e minimo è (21.4+28.6)=50 = 2 x 25. Quindi è confermata la amplificazione del fattore 2.5 sul valore dello spostamento applicato staticamente.
•Il lasso di tempo corrispondente a un semi-periodo è pari a (0.906-0.846)=0.06 = T/2, nei limiti delle cifre significative disponibili.
•L'andamento è sinusoidale, e si stabilizza come predetto dalla teoria.
•Lo spostamento corrispondente alla applicazione del carico statico, corrispondente al tempo t=0, è pari a 3628.56 N/ 1000 (N/mm) = 3.628 mm --> 3.63 mm.
•Analogo spostamento hanno il nodo in mezzeria e alla altra estremità, a conferma che il movimento è traslatorio.
Una analisi di questo tipo non si sarebbe potuta fare con la time history modale, perché, a causa della presenza di smorzatori concentrati, di fatto sovrapposti alle molle, il sistema non sarebbe stato disaccoppiabile. Invece, con la integrazione diretta del sistema, e il corretto assemblaggio alla matrice di smorzamento C dei contributi degli elementi, il sistema è stato risolto.